LU分解法求解线性方程组
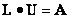 (1)
(1)
 (2)
(2)
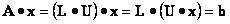 (3)
(3)
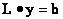 (4)
(4)
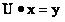 (5)
(5)
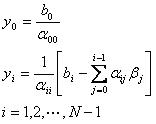 (6)
(6)
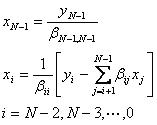 (7)
(7)
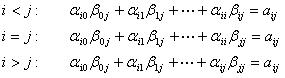 (8,9,10)
(8,9,10)
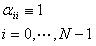 (11)
(11)
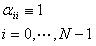 ,即(11)式
,即(11)式
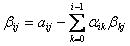 (12)
(12)
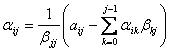 (13)
(13)

 package com.nc4nr.chapter02.lu;
package com.nc4nr.chapter02.lu;

 public class LU ...{
public class LU ...{
 // 4 * 4 coefficient matrix a
// 4 * 4 coefficient matrix a
 double[][] a = ...{
double[][] a = ...{
 ...{0.0, 2.0, 0.0, 1.0},
...{0.0, 2.0, 0.0, 1.0},
 ...{2.0, 2.0, 3.0, 2.0},
...{2.0, 2.0, 3.0, 2.0},
 ...{4.0, -3.0, 0.0, 1.0},
...{4.0, -3.0, 0.0, 1.0},
 ...{6.0, 1.0, -6.0, -5.0}
...{6.0, 1.0, -6.0, -5.0} };
};
 // 4 * 1 coefficient matrix b
// 4 * 1 coefficient matrix b
 double[] b = ...{
double[] b = ...{ 0.0,
0.0, -2.0,
-2.0, -7.0,
-7.0, 6.0
6.0 };
};
 int anrow = 4;
int anrow = 4; int[] indx = new int[anrow];
int[] indx = new int[anrow]; int parity = 1;
int parity = 1;

 private void lucmp() ...{
private void lucmp() ...{ final double tiny = 1.0e-20;
final double tiny = 1.0e-20; int imax = 0, n = anrow;
int imax = 0, n = anrow; double big, dum, sum, temp;
double big, dum, sum, temp; double[] vv = new double[n];
double[] vv = new double[n];
 System.out.println("Origin coefficient matrix:");
System.out.println("Origin coefficient matrix:"); output(a,4);
output(a,4);

 for (int i = 0; i < n; i++) ...{
for (int i = 0; i < n; i++) ...{ big = 0.0;
big = 0.0;
 for (int j = 0; j < n; j++) ...{
for (int j = 0; j < n; j++) ...{ if ((temp = Math.abs(a[i][j])) > big) big = temp;
if ((temp = Math.abs(a[i][j])) > big) big = temp; }
} if (big == 0.0) System.out.println("lu: singular matrix in lucmp.");
if (big == 0.0) System.out.println("lu: singular matrix in lucmp."); vv[i] = 1.0/big;
vv[i] = 1.0/big; }
}

 for (int j = 0; j < n; j++) ...{
for (int j = 0; j < n; j++) ...{
 for (int i = 0; i < j; i++) ...{
for (int i = 0; i < j; i++) ...{ sum = a[i][j];
sum = a[i][j]; for (int k = 0; k < i; k++) sum -= a[i][k]*a[k][j];
for (int k = 0; k < i; k++) sum -= a[i][k]*a[k][j]; a[i][j] = sum;
a[i][j] = sum; }
} big = 0.0;
big = 0.0;
 for (int i = j; i < n; i++) ...{
for (int i = j; i < n; i++) ...{ sum = a[i][j];
sum = a[i][j]; for (int k = 0; k < j; k++) sum -= a[i][k]*a[k][j];
for (int k = 0; k < j; k++) sum -= a[i][k]*a[k][j]; a[i][j] = sum;
a[i][j] = sum;
 if ((dum = vv[i]*Math.abs(sum)) >= big) ...{
if ((dum = vv[i]*Math.abs(sum)) >= big) ...{ big = dum;
big = dum; imax = i;
imax = i; }
} }
}
 if (j != imax) ...{
if (j != imax) ...{
 for(int k = 0; k < n; k++) ...{
for(int k = 0; k < n; k++) ...{ dum = a[imax][k];
dum = a[imax][k]; a[imax][k] = a[j][k];
a[imax][k] = a[j][k]; a[j][k] = dum;
a[j][k] = dum; }
} parity = -parity;
parity = -parity; dum = vv[imax];
dum = vv[imax]; vv[imax] = vv[j];
vv[imax] = vv[j]; vv[j] = dum;
vv[j] = dum; }
} indx[j] = imax;
indx[j] = imax; if (a[j][j] == 0.0) a[j][j] = tiny;
if (a[j][j] == 0.0) a[j][j] = tiny;
 if (j != n - 1) ...{
if (j != n - 1) ...{ dum = 1.0/a[j][j];
dum = 1.0/a[j][j]; for (int i = j+1; i < n; i++) a[i][j] *= dum;
for (int i = j+1; i < n; i++) a[i][j] *= dum; }
} }
}
 System.out.println("LU mixed matrix:");
System.out.println("LU mixed matrix:"); output(a,4);
output(a,4); }
}

 private void lubksb() ...{
private void lubksb() ...{ double sum;
double sum; int n = anrow, ii = 0;
int n = anrow, ii = 0;
 System.out.println("Origin left-hand vector b:");
System.out.println("Origin left-hand vector b:"); output(b,4);
output(b,4);

 for (int i = 0; i < n; i++) ...{
for (int i = 0; i < n; i++) ...{ int ip = indx[i];
int ip = indx[i]; sum = b[ip];
sum = b[ip]; b[ip] = b[i];
b[ip] = b[i]; if (ii != 0)
if (ii != 0) for (int j = ii - 1; j < i; j++) sum -= a[i][j]*b[j];
for (int j = ii - 1; j < i; j++) sum -= a[i][j]*b[j]; else if (sum != 0.0)
else if (sum != 0.0)  ii = i + 1;
ii = i + 1; b[i] = sum;
b[i] = sum; }
}
 for (int i = n-1; i >= 0; i--) ...{
for (int i = n-1; i >= 0; i--) ...{ sum = b[i];
sum = b[i]; for(int j = i + 1; j < n; j++) sum -= a[i][j]*b[j];
for(int j = i + 1; j < n; j++) sum -= a[i][j]*b[j]; b[i] = sum / a[i][i];
b[i] = sum / a[i][i]; }
} System.out.println("Final solution vector:");
System.out.println("Final solution vector:"); output(b,4);
output(b,4); }
}

 private void output(double a[][], int anrow) ...{
private void output(double a[][], int anrow) ...{
 for (int i = 0; i < anrow; i++) ...{
for (int i = 0; i < anrow; i++) ...{ System.out.println(" | " + a[i][0] + " " +
System.out.println(" | " + a[i][0] + " " +  a[i][1] + " " +
a[i][1] + " " +  a[i][2] + " " +
a[i][2] + " " +  a[i][3] + " | ");
a[i][3] + " | "); }
} System.out.println("-----------------------------------------------");
System.out.println("-----------------------------------------------"); }
}

 private void output(double[] b, int bnrow) ...{
private void output(double[] b, int bnrow) ...{
 for (int i = 0; i < bnrow; i++) ...{
for (int i = 0; i < bnrow; i++) ...{ System.out.println(" | " + b[i] + " | ");
System.out.println(" | " + b[i] + " | "); }
} System.out.println("-----------------------------------------------");
System.out.println("-----------------------------------------------"); }
}

 public LU() ...{
public LU() ...{ lucmp(); // 分解
lucmp(); // 分解 lubksb(); // 回代
lubksb(); // 回代 }
}

 public static void main(String[] args) ...{
public static void main(String[] args) ...{ new LU();
new LU(); }
}
 }
}
LU分解法求解线性方程组相关推荐
- matlab lu解线性方程,MATLAB报告用LU分解法求解线性方程组.doc
MATLAB报告用LU分解法求解线性方程组 <MATLAB>期末大报告 报告内容:用LU分解法求解线性方程组 学院(系): 专 业: 班 级: 学 号: 学生姓名: 2014 年 6 月 ...
- Matlab实现 LU分解法解线性方程组(全选主元列选主元)
选主元LU分解 实验内容:列选主元LU分解和全选主元LU分解求解线性方程组 计算方法: 全选主元消元法 1.1 初始化 根据参数A.b,记录下矩阵.右端项的尺寸n: 以得到的尺寸n初始化解向量x: 同 ...
- 数值分析3-解线性方程组的高斯消去法、LU分解法及列主元消去法的matlab程序和调试方法
对于形如Ax=b的线性方程组,在线性代数中是通过求逆的方式求解的,即x=A-1b,而在数值分析中,解线性方程组的方法是通过直接法或者迭代法来实现的,今天写的三个程序都属于直接法,分别为高斯消去法.LU ...
- 紧凑存储的杜利特尔分解法Doolittle(LU分解法)_解线性方程组的直接解法
紧凑存储的杜利特尔分解法Doolittle(LU分解法)_解线性方程组的直接解法 标签:计算方法实验 /* 紧凑存储的杜利特尔分解法Doolittle:如果初始矩阵不要求保留的话,可以紧凑存储.因为每 ...
- 解线性方程组的直接方法:LU分解法及其C语言算法实现
在上一篇博客里面,笔者介绍了解线性方程组的列主元Guass消元法,这篇将介绍LU分解法及其算法实现. 什么是LU分解? 对于一个线性方程组Ax=b,其中A是非奇异系数矩阵,b是线性方程组右端项,在列主 ...
- Doolittle分解法(LU分解法)的Python实现
在解一般的非奇异矩阵线性方程组的时候,或者在迭代改善算法中,需要使用LU分解法. 对于一个一般的非奇异矩阵A=(a11, a12,-,a1n,a21,-ann),可分解为一个下三角矩阵L和一个上三角矩 ...
- Matlab | Lab4——用LU 分解法、 Jacobi 迭代、 Gauss-Seidel 迭代 解线性病态方程组(系数矩阵为Hilbert矩阵)
1.要求 考虑线性方程组Hx=b,其中H为n阶Hilbert矩阵,即 通过先给定解(例如取x的各个分量为1),再计算出右端向量b的办法给出一个精确解已知的问题. (1)分别编写Doolittle LU ...
- 乔列斯基分解法求线性方程组的MATLAB程序实现
编写的 乔列斯基分解算法的MATLAB 程序如下: 功能:LL分解法求线性方程组AX=b的解调用格式:[X,L]= SymPosl (A,b) 其中, A:线性方程组的系数矩阵: b:线性方程组的常数 ...
- LU分解法 | matlab
% LU分解法 % M为输入的增广矩阵 % precision为输入的精度要求,如不输入或输入有误,则默认为10位if nargin == 2trydigits(precision);catchdis ...
- Python02 雅克比迭代法 Gauss-Seidel迭代法 列选主元法 LU分解法(附代码)
1. 实验结果 (1)在定义的矩阵类中设置需要求解的方程为: (2)在 test.py 中选择雅克比迭代法求解: 输入:最大容许迭代次数和精度要求: 输出:根据谱半径判断方法是否收敛,收敛时得到满足精 ...
最新文章
- C++ 函数模板和排序的函数模板——学习笔记
- html5语音对讲,c#语音对讲demo
- 弱引用使用场景桌面_吃透Java基础十五:强引用、软引用、弱引用、虚引用
- Linux原始套接字学习总结
- SAP收发存报表程序
- 数学猜想验证步骤_高中数学解题思路与技巧汇总,19种解题方法,实用!
- 在PS中如何进行图文互排,且层的使用……
- LaTex ——P4 字体字号设置
- oracle添加联合主键
- python中怎样划分时间段_如何划分重叠的日期时间间隔(组织模式时钟时间)?...
- 工具分享:xampp-windows-x64-7.3.2-1-VC15-installer.exe 请自行下载(附下载链接)
- Java飞机大战 项目-源码
- bootstrap实现树节点、树结构
- Web前端学习路线笔记(六)html5
- 用易升升级到Win10后在第三方浏览器无法打开网页的解决办法
- python去除pdf水印_聊聊 Python 操作PDF的几种方法(合并、拆分、水印、加密)
- Python实现自动给视频打码,减少不宜画面出现...
- android gms认证之run host test,Android GMS认证项总结
- numpy.arange()参数含义
- 安卓app单webview改为多webview加载网页
