A Visual, Intuitive Guide to Imaginary Numbers
2019独角兽企业重金招聘Python工程师标准>>> 
maginary numbers always confused me. Like understanding e, most explanations fell into one of two categories:
It’s a mathematical abstraction, and the equations work out. Deal with it.
It’s used in advanced physics, trust us. Just wait until college.
Gee, what a great way to encourage math in kids! Today we’ll assault this topic with our favorite tools:
Focusing on relationships, not mechanical formulas.
Seeing complex numbers as an upgrade to our number system, just like zero, decimals and negatives were.
Using visual diagrams, not just text, to understand the idea.
And our secret weapon: learning by analogy. We’ll approach imaginary numbers by observing its ancestor, the negatives. Here’s your guidebook:
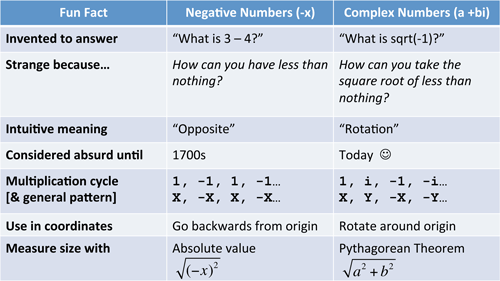
It doesn’t make sense yet, but hang in there. By the end we’ll hunt down i and put it in a headlock, instead of the reverse.
Video Walkthrough:
Really Understanding Negative Numbers
Negative numbers aren’t easy. Imagine you’re a European mathematician in the 1700s. You have 3 and 4, and know you can write 4 – 3 = 1. Simple.
But what about 3-4? What, exactly, does that mean? How can you take 4 cows from 3? How could you have less than nothing?
Negatives were considered absurd, something that “darkened the very whole doctrines of the equations” (Francis Maseres, 1759). Yet today, it’d be absurd to think negatives aren’t logical or useful. Try asking your teacher whether negatives corrupt the very foundations of math.
What happened? We invented a theoretical number that had useful properties. Negatives aren’t something we can touch or hold, but they describe certain relationships well (like debt). It was a useful fiction.
Rather than saying “I owe you 30” and reading words to see if I’m up or down, I can write “-30” and know it means I’m in the hole. If I earn money and pay my debts (-30 + 100 = 70), I can record the transaction easily. I have +70 afterwards, which means I’m in the clear.
The positive and negative signs automatically keep track of the direction — you don’t need a sentence to describe the impact of each transaction. Math became easier, more elegant. It didn’t matter if negatives were “tangible” — they had useful properties, and we used them until they became everyday items. Today you’d call someone obscene names if they didn’t “get” negatives.
But let’s not be smug about the struggle: negative numbers were a huge mental shift. Even Euler, the genius who discovered e and much more, didn’t understand negatives as we do today. They were considered “meaningless” results (he later made up for this in style).
It’s a testament to our mental potential that today’s children are expected to understand ideas that once confounded ancient mathematicians.
Enter Imaginary Numbers
Imaginary numbers have a similar story. We can solve equations like this all day long:
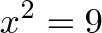
The answers are 3 and -3. But suppose some wiseguy puts in a teensy, tiny minus sign:
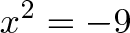
Uh oh. This question makes most people cringe the first time they see it. You want the square root of a number less than zero? That’s absurd! (Historically, there were real questions to answer, but I like to imagine a wiseguy.)
It seems crazy, just like negatives, zero, and irrationals (non-repeating numbers) must have seemed crazy at first. There’s no “real” meaning to this question, right?
Wrong. So-called “imaginary numbers” are as normal as every other number (or just as fake): they’re a tool to describe the world. In the same spirit of assuming -1, .3, and 0 “exist”, let’s assume some number i exists where:
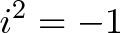
That is, you multiply i by itself to get -1. What happens now?
Well, first we get a headache. But playing the “Let’s pretend i exists” game actually makes math easier and more elegant. New relationships emerge that we can describe with ease.
You may not believe in i, just like those fuddy old mathematicians didn’t believe in -1. New, brain-twisting concepts are hard and they don’t make sense immediately, even for Euler. But as the negatives showed us, strange concepts can still be useful.
I dislike the term “imaginary number” — it was considered an insult, a slur, designed to hurt i‘s feelings. The number i is just as normal as other numbers, but the name “imaginary” stuck so we’ll use it.
Visual Understanding of Negative and Complex Numbers
As we saw last time, the equation x^2 = 9 really means:
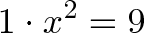
or
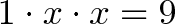
What transformation x, when applied twice, turns 1 to 9?
The two answers are “x = 3” and “x = -3”: That is, you can “scale by” 3 or “scale by 3 and flip” (flipping or taking the opposite is one interpretation of multiplying by a negative).
Now let’s think about x^2 = -1, which is really
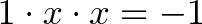
What transformation x, when applied twice, turns 1 into -1? Hrm.
We can’t multiply by a positive twice, because the result stays positive
We can’t multiply by a negative twice, because the result will flip back to positive on the second multiplication
But what about… a rotation! It sounds crazy, but if we imagine x being a “rotation of 90 degrees”, then applying x twice will be a 180 degree rotation, or a flip from 1 to -1!
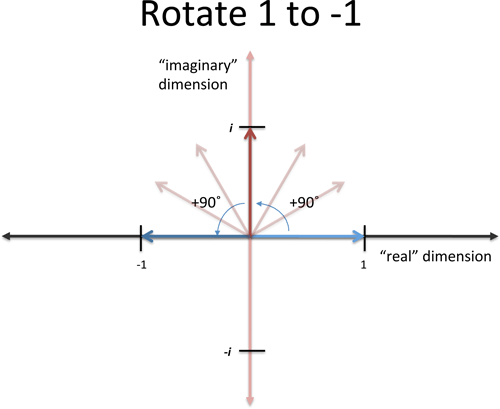
Yowza! And if we think about it more, we could rotate twice in the other direction (clockwise) to turn 1 into -1. This is “negative” rotation or a multiplication by -i:
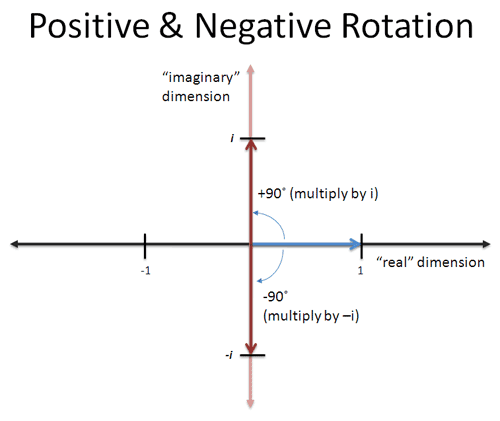
If we multiply by -i twice, the first multiplication would turn 1 into -i, and the second turns -i into -1. So there’s really two square roots of -1: i and -i.
This is pretty cool. We have some sort of answer, but what does it mean?
i is a “new imaginary dimension” to measure a number
i (or -i) is what numbers “become” when rotated
Multiplying i is a rotation by 90 degrees counter-clockwise
Multiplying by -i is a rotation of 90 degrees clockwise
Two rotations in either direction is -1: it brings us back into the “regular” dimensions of positive and negative numbers.
Numbers are 2-dimensional. Yes, it’s mind bending, just like decimals or long division would be mind-bending to an ancient Roman. (What do you mean there’s a number between 1 and 2?). It’s a strange, new way to think about math.
We asked “How do we turn 1 into -1 in two steps?” and found an answer: rotate it 90 degrees. It’s a strange, new way to think about math. But it’s useful. (By the way, this geometric interpretation of complex numbers didn’t arrive until decades after i was discovered).
Also, keep in mind that having counter-clockwise be positive is a human convention — it easily could have been the other way.
Finding Patterns
Let’s dive into the details a bit. When multiplying negative numbers (like -1), you get a pattern:
1, -1, 1, -1, 1, -1, 1, -1
Since -1 doesn’t change the size of a number, just the sign, you flip back and forth. For some number “x”, you’d get:
x, -x, x, -x, x, -x…
This idea is useful. The number “x” can represent a good or bad hair week. Suppose weeks alternate between good and bad; this is a good week; what will it be like in 47 weeks?

So -x means a bad hair week. Notice how negative numbers “keep track of the sign” — we can throw (-1)^47 into a calculator without having to count (”Week 1 is good, week 2 is bad… week 3 is good…“). Things that flip back and forth can be modeled well with negative numbers.
Ok. Now what happens if we keep multiplying by i?

Very funny. Let’s reduce this a bit:
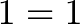 (No questions here)
(No questions here) (Can’t do much)
(Can’t do much)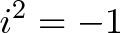 (That’s what i is all about)
(That’s what i is all about)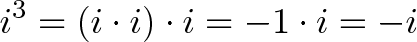 (Ah, 3 rotations counter-clockwise = 1 rotation clockwise. Neat.)
(Ah, 3 rotations counter-clockwise = 1 rotation clockwise. Neat.) (4 rotations bring us “full circle”)
(4 rotations bring us “full circle”) (Here we go again…)
(Here we go again…)
Represented visually:
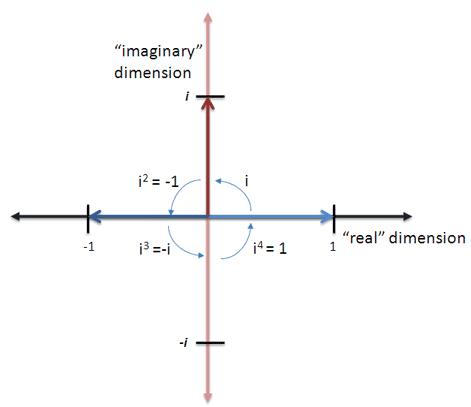
We cycle every 4th rotation. This makes sense, right? Any kid can tell you that 4 left turns is the same as no turns at all. Now rather than focusing on imaginary numbers (i, i^2), look at the general pattern:
X, Y, -X, -Y, X, Y, -X, -Y…
Like negative numbers modeling flipping, imaginary numbers can model anything that rotates between two dimensions “X” and “Y”. Or anything with a cyclic, circular relationship — have anything in mind?
‘Cos it’d be a sin if you didn’t. There’ll de Moivre be more in future articles. [Editor’s note: Kalid is in electroshock therapy to treat his pun addiction.]
Understanding Complex Numbers
There’s another detail to cover: can a number be both “real” and “imaginary”?
You bet. Who says we have to rotate the entire 90 degrees? If we keep 1 foot in the “real” dimension and another in the imaginary one, it looks like this:

We’re at a 45 degree angle, with equal parts in the real and imaginary (1 + i). It’s like a hotdog with both mustard and ketchup — who says you need to choose?
In fact, we can pick any combination of real and imaginary numbers and make a triangle. The angle becomes the “angle of rotation”. A complex number is the fancy name for numbers with both real and imaginary parts. They’re written a + bi, where
a is the real part
b is the imaginary part

Not too bad. But there’s one last question: how “big” is a complex number? We can’t measure the real part or imaginary parts in isolation, because that would miss the big picture.
Let’s step back. The size of a negative number is not whether you can count it — it’s the distance from zero. In the case of negatives this is:
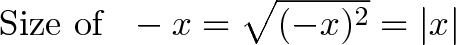
Which is another way to find the absolute value. But for complex numbers, how do we measure two components at 90 degree angles?
It’s a bird… it’s a plane… it’s Pythagoras!
Geez, his theorem shows up everywhere, even in numbers invented 2000 years after his time. Yes, we are making a triangle of sorts, and the hypotenuse is the distance from zero:

Neat. While measuring the size isn’t as easy as “dropping the negative sign”, complex numbers do have their uses. Let’s take a look.
A Real Example: Rotations
We’re not going to wait until college physics to use imaginary numbers. Let’s try them outtoday. There’s much more to say about complex multiplication, but keep this in mind:
Multiplying by a complex number rotates by its angle
Let’s take a look. Suppose I’m on a boat, with a heading of 3 units East for every 4 units North. I want to change my heading 45 degrees counter-clockwise. What’s the new heading?

Some hotshot will say “That’s simple! Just take the sine, cosine, gobbledegook by the tangent… fluxsom the foobar… and…“. Crack. Sorry, did I break your calculator? Care to answer that question again?
Let’s try a simpler approach: we’re on a heading of 3 + 4i (whatever that angle is; we don’t really care), and want to rotate by 45 degrees. Well, 45 degrees is 1 + i (perfect diagonal), so we can multiply by that amount!
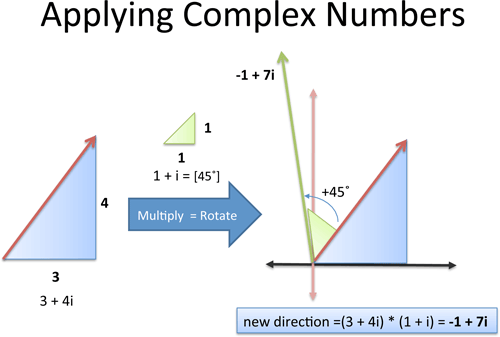
Here’s the idea:
Original heading: 3 units East, 4 units North = 3 + 4i
Rotate counter-clockwise by 45 degrees = multiply by 1 + i
If we multiply them together we get:
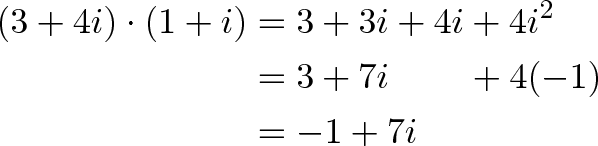
So our new orientation is 1 unit West (-1 East), and 7 units North, which you could draw out and follow.
But yowza! We found that out in 10 seconds, without touching sine or cosine. There were no vectors, matrices, or keeping track what quadrant we are in. It was just arithmetic with a touch of algebra to cross-multiply. Imaginary numbers have the rotation rules baked in:it just works.
Even better, the result is useful. We have a heading (-1, 7) instead of an angle (atan(7/-1) = 98.13, keeping in mind we’re in quadrant 2). How, exactly, were you planning on drawing and following that angle? With the protractor you keep around?
No, you’d convert it into cosine and sine (-.14 and .99), find a reasonable ratio between them (about 1 to 7), and sketch out the triangle. Complex numbers beat you to it, instantly, accurately, and without a calculator.
If you’re like me, you’ll find this use mind-blowing. And if you don’t, well, I’m afraid math doesn’t toot your horn. Sorry.
Trigonometry is great, but complex numbers can make ugly calculations simple (like calculating cosine(a+b) ). This is just a preview; later articles will give you the full meal.
Aside: Some people think “Hey, it’s not useful to have North/East headings instead of a degree angle to follow!”
Really? Ok, look at your right hand. What’s the angle from the bottom of your pinky to the top of your index finger? Good luck figuring that out on your own.
With a heading, you can at least say “Oh, it’s X inches across and Y inches up” and have some chance of working with that bearing.
Complex Numbers Aren’t
That was a whirlwind tour of my basic insights. Take a look at the first chart — it should make sense now.
There’s so much more to these beautiful, zany numbers, but my brain is tired. My goals were simple:
Convince you that complex numbers were considered “crazy” but can be useful (just like negative numbers were)
Show how complex numbers can make certain problems easier, like rotations
If I seem hot and bothered about this topic, there’s a reason. Imaginary numbers have been a bee in my bonnet for years — the lack of an intuitive insight frustrated me.
Now that I’ve finally had insights, I’m bursting to share them. But it frustrates me that you’re reading this on the blog of a wild-eyed lunatic, and not in a classroom. We suffocate our questions and “chug through” — because we don’t search for and share clean, intuitive insights. Egad.
But better to light a candle than curse the darkness: here’s my thoughts, and one of you will shine a spotlight. Thinking we’ve “figured out” a topic like numbers is what keeps us in Roman Numeral land.
There’s much more complex numbers: check out the details of complex arithmetic. Happy math.
Epilogue: But they’re still strange!
I know, they’re still strange to me too. I try to put myself in the mind of the first person to discover zero.
Zero is such a weird idea, having “something” represent “nothing”, and it eluded the Romans. Complex numbers are similar — it’s a new way of thinking. But both zero and complex numbers make math much easier. If we never adopted strange, new number systems, we’d still be counting on our fingers.
I repeat this analogy because it’s so easy to start thinking that complex numbers aren’t “normal”. Let’s keep our mind open: in the future they’ll chuckle that complex numbers were once distrusted, even until the 2000’s.
If you want more nitty-gritty, check out wikipedia, the Dr. Math discussion, or another argument on why imaginary numbers exist.
Other Posts In This Series
A Visual, Intuitive Guide to Imaginary Numbers
Intuitive Guide to Angles, Degrees and Radians
Intuitive Arithmetic With Complex Numbers
Understanding Why Complex Multiplication Works
Intuitive Understanding Of Euler's Formula
An Interactive Guide To The Fourier Transform
Intuitive Understanding of Sine Waves
An Intuitive Guide to Linear Algebra
转载于:https://my.oschina.net/jjyuangu/blog/525941
A Visual, Intuitive Guide to Imaginary Numbers相关推荐
- An Intuitive Guide to Optimal Transport|最优传输理论
An Intuitive Guide to Optimal Transport|最优传输理论 最优传输:最优传输问题最早是由法国数学家蒙日于1780年代提出:其解的存在性被俄国数学家Kantorovi ...
- 正式举报林-裴 (1999) 论文涉嫌学术不端
发件人: Transmissome <yrao@pku.edu.cn> 日期: Thursday, January 21, 2021 at 10:25 PM 至: Gang Pei < ...
- 数据管理,数据治理,数据中心,数据中台,数据湖这下就分清楚了!
随着信息技术的不断涌现和普及,业务发展加快了数据膨胀的速度,行业内衍生了较多的新名词,如数据治理.数据管理.数据资源管理.数据资产管理等名词的定义很多,概念容易混淆,本文对这些名词术语及内涵进行系统的 ...
- 45 年编程经验告诉我的技术真相
一位在软件开发行业兢兢业业工作了 45 年的老程序员,在退休之际,分享了他的一些值得我们借鉴和学习的经验,希望能对各位有所启发. >>>> 01 千万不要被知识蒙蔽双眼 在掌握 ...
- 好书 python_[好书首发]Python-Visual Quickstart Guide(第三版,最新版)
Python培训 更多好资料可以关注我哦 +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Pytho ...
- 资源 | 机器学习、NLP、Python和Math最好的150余个教程(建议收藏)
编辑 | MingMing 尽管机器学习的历史可以追溯到1959年,但目前,这个领域正以前所未有的速度发展.最近,我一直在网上寻找关于机器学习和NLP各方面的好资源,为了帮助到和我有相同需求的人,我整 ...
- 超过 150 个最佳机器学习,NLP 和 Python教程
作者:chen_h 微信号 & QQ:862251340 微信公众号:coderpai 我的博客:请点击这里 我把这篇文章分为四个部分:机器学习,NLP,Python 和 数学.我在每一部分都 ...
- 卷积神经网络学习指南_卷积神经网络的直观指南
卷积神经网络学习指南 by Daphne Cornelisse 达芙妮·康妮莉丝(Daphne Cornelisse) 卷积神经网络的直观指南 (An intuitive guide to Convo ...
- ICLR2020国际会议焦点论文(Spotlight Paper)列表(内含论文源码)
来源:AINLPer微信公众号(点击了解一下吧) 编辑: ShuYini 校稿: ShuYini 时间: 2020-02-21 2020年的ICLR会议将于今年的4月26日-4月30日在Mil ...
- 超级大汇总!200多个最好的机器学习、NLP和Python教程
这篇文章包含了我目前为止找到的最好的教程内容.这不是一张罗列了所有网上跟机器学习相关教程的清单--不然就太冗长太重复了.我这里并没有包括那些质量一般的内容.我的目标是把能找到的最好的教程与机器学习和自 ...
最新文章
- Android ImageView的ScaleType属性
- linux删除静态arp,Linux如何清理ARP缓存?
- openvas-tutorial-for-beginners
- jsonp 使用选择器
- [译] 为什么需要在 React 类组件中为事件处理程序绑定 this
- 基于python的手机销售系统
- 十年后的我们会是什么样的呢,二十年后的我国 会是什么样呢
- 内网虚拟机静态IP设置VMWare内网通外网不通把某一网段白名单虚拟机ping不通主机虚拟机桥接改成非192.168网段服务器与电脑直连共享wifi
- WFD抓包及视频提取
- 手机玻璃盖板玻璃logo字符丝印视觉检测系统
- echarts 立体柱状图(多个柱状图)
- 《概率论与数理统计》之样本空间和随机事件
- 字符串格式化:Formatter类
- pap.er - Mac必备5K壁纸下载软件
- 基于安卓的掌上校园系统|食堂缴费图书馆预约【可微信小程序与android studio运行】
- 判断字符串是否是英文
- php 如何播放wav,Php标题为.wav文件下载但无法在嵌入中播放
- 逆天了!ChatGPT回答癌症问题,准确性与美国国家癌症研究所标准答案不相上下...
- Android 应用崩溃日志的收集和上传
- JAVA中面向对象基础:抽象类、初始化块
热门文章
- RGB, YUV及相关标准
- Python学习笔记--解析式
- 关于反病毒技术的想法
- 测试常见面试题,如何有效的做自我介绍
- ECCV2020:论文解读《Synthesize then Compare: Detecting Failures and Anomalies for Semantic Segmentation》
- C#读写内存也不差!(发布C#编写的植物大战僵尸作弊器源码)
- 中线提取算法_一种应用VisualGraph算法提取道路中线的方法与流程
- CTeX 中文 beamer 模板
- 为什么一个还没毕业的大学生能够把 IO 讲的这么好?
- vs2017工具箱问题(不见工具箱选项卡此组中没有可用控件控件灰化)
