CH4：Recurrences

Review：

MergeSort
分析MergeSort的时间复杂度
- 递归树 Picture of Recursion Tree
- 迭代法 Telescoping
- 数学归纳法 Mathematical Induction
渐近分析
- O − N o t a t i o n O-Notation O−Notation
- Ω − N o t a t i o n \Omega-Notation Ω−Notation
- Θ − N o t a t i o n \Theta-Notation Θ−Notation

算法包含对自身的调用时，其运行时间可以用递归式表示：

M e r g e S o r t ： T ( n ) = a T ( n / b ) + D ( n ) + C ( n ) = 2 T ( n / 2 ) + O ( n ) MergeSort：T(n) = aT(n/b) +D(n) +C(n) = 2T(n/2) + O(n) MergeSort：T(n)=aT(n/b)+D(n)+C(n)=2T(n/2)+O(n)

3种求解递归函数的方法：

代换法-------------Substitution
递归树法----------Recursion Tree
主方法-------------Master Method

4.1 Substitution Method 代换法

（1）步骤

步骤：

猜测一个解的形式 Guess the form of solution
使用数学归纳法证明 Verify by induction
求解常数项 Solve for constants

（2）例子

Example1： T ( n ) = 4 T ( n / 2 ) + 100 n T(n) = 4T(n/2) + 100n T(n)=4T(n/2)+100n

猜测： O ( n 3 ) O(n^3) O(n3)（如果要证明 Θ \Theta Θ的话，那么要分别证明O和 Ω \Omega Ω）

归纳基础： T ( 1 ) = Θ ( 1 ) T(1) = \Theta(1) T(1)=Θ(1)

归纳假设：$T(k) \leq ck^3 在在在k < n$时成立

使用数学归纳法证明： T ( n ) ≤ c n 3 T(n) \leq cn^3 T(n)≤cn3

证明：
T ( n ) = 4 T ( n / 2 ) + 100 n ≤ 4 c ( n / 2 ) 3 + 100 n = ( c / 2 ) n 3 + 100 n = c n 3 − ( ( c / 2 ) n 3 − 100 n ) ≤ c n 3 \begin{aligned} \mathrm{T}(\mathrm{n}) &=4 \mathrm{~T}(\mathrm{n} / 2)+100 n \\ & \leq 4 \mathrm{c}(\mathrm{n} / 2)^{3}+100 n \\ &=(\mathrm{c} / 2) n^{3}+100 n \\ &=\mathrm{cn}^{3}-\left((\mathrm{c} / 2) n^{3}-100 n\right)\\ &\leq\mathrm{cn}^{3} \end{aligned} T(n)=4 T(n/2)+100n≤4c(n/2)3+100n=(c/2)n3+100n=cn3−((c/2)n3−100n)≤cn3
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uT0feEXC-1654484649510)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220605163554811.png)]

最后确定c和n的值即可：

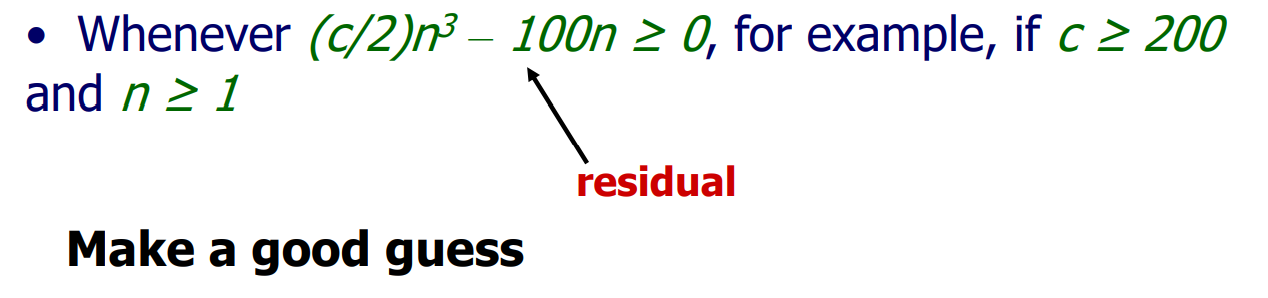
Example2： T ( n ) = 2 T ( ⌊ n / 2 ⌋ ) + n T(n) = 2T(\lfloor n/2\rfloor) + n T(n)=2T(⌊n/2⌋)+n

要严格遵守证明的结果的模式，下面的证明是错误的：

Example3：尝试变量替换

考虑： T ( n ) = 2 T ( n ) + l g n T(n) = 2T(\sqrt{n}) + lgn T(n)=2T(n )+lgn
Rename： m = l g n ⇒ T ( 2 m ) = 2 T ( 2 m 2 ) + m m = lgn\Rightarrow T(2^m) = 2T(2^{\frac{m}{2}})+m m=lgn⇒T(2m)=2T(22m)+m
令 S ( m ) = T ( 2 m ) S(m) = T(2^m) S(m)=T(2m)，则有： S ( m ) = 2 S ( m / 2 ) + m S(m) = 2S(m/2) + m S(m)=2S(m/2)+m

设当 m 0 ≤ m m_0\leq m m0≤m时有： S ( m 0 ) ≤ c m 0 l g m 0 S(m_0)\leq cm_0lgm_0 S(m0)≤cm0lgm0
S ( m ) = 2 S ( m / 2 ) + m ≤ 2 c ( m / 2 ) l g ( m / 2 ) + m = c m l g ( m / 2 ) + m = c m l g m − c m + m = c m l g m − ( c − 1 ) m = O ( m l g m ) S(m) = 2S(m/2) + m\\ \leq 2c(m/2)lg(m/2) + m\\ =cmlg(m/2)+m\\=cmlgm-cm + m\\ =cmlgm-(c-1)m\\=O(mlgm) S(m)=2S(m/2)+m≤2c(m/2)lg(m/2)+m=cmlg(m/2)+m=cmlgm−cm+m=cmlgm−(c−1)m=O(mlgm)
转换回来

T ( 2 m ) = S ( m ) = O ( m l g m ) T(2^m) = S(m) = O(mlgm) T(2m)=S(m)=O(mlgm)

T ( m ) = O ( l g m l g m ) T(m) = O(lgmlgm) T(m)=O(lgmlgm)

T ( n ) = O ( l g n l g l g n ) T(n) = O(lgnlglgn) T(n)=O(lgnlglgn)

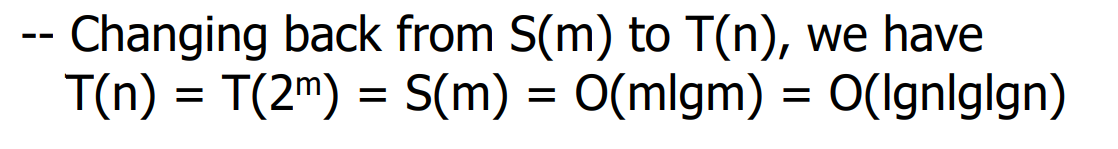
（3）猜测方法

使用代换法的一个重要技巧是要猜测

猜测的方式：

递归树的方法帮助猜测
与先前见过的相似
先整较松的上届然后缩小区间

降低上届，提高下界，缩小不确定区间

4.2 Recursion-tree Method

递归树是一个好的猜测的直接方法

递归树方法可能不可靠，就像任何使用省略号的方法一样

4.2.1 例子说明

T ( n ) = 3 T ( n / 4 ) + Θ ( n 2 ) T(n) = 3T(n/4) + \Theta(n^2) T(n)=3T(n/4)+Θ(n2)

（1）递归树猜测上界

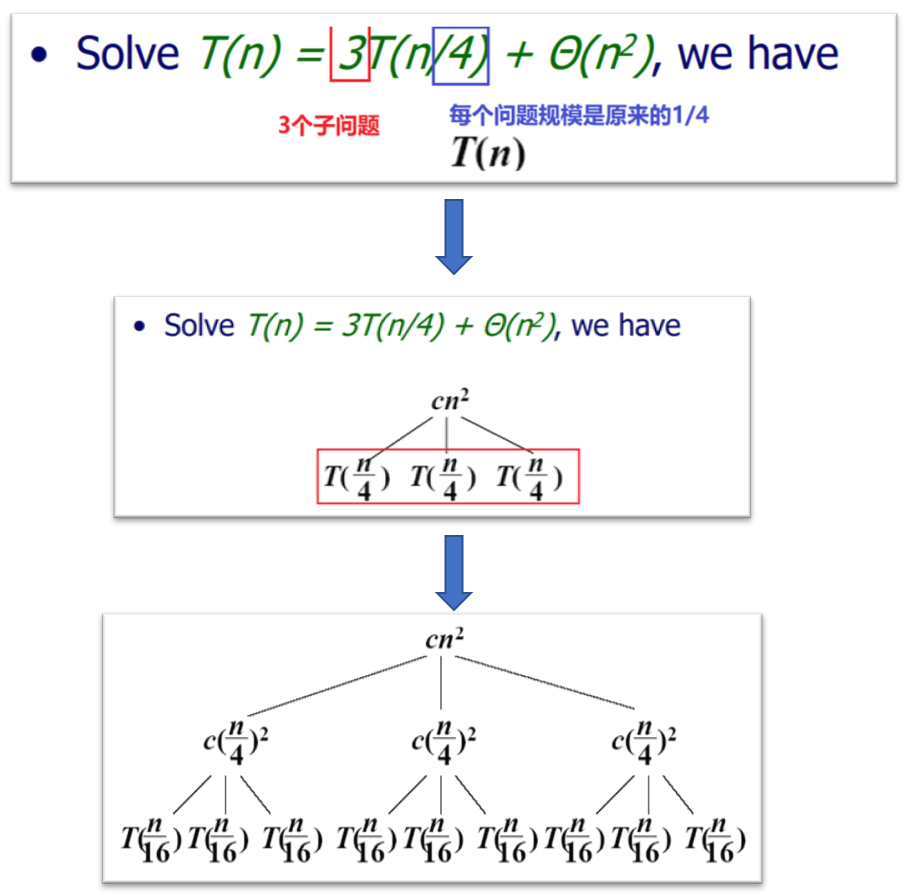
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Iw1tuwUO-1654484649511)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20220605175243692.png)]

最后一层叶子数： 3 l o g 4 n = n l o g 4 3 3^{log_4^n} = n^{log_4^3} 3log4n=nlog43
每层开销： ( ( 3 16 ) i c n 2 ) ((\frac{3}{16})^icn^2) ((163)icn2)
总开销： c n 2 + ( 3 16 ) c n 2 + ( 3 16 ) 2 c n 2 + . . . . . . + ( 3 16 ) l o g 4 n − 1 c n 2 + O ( n l o g 4 3 ) = 1 × ( 1 − ( 3 16 ) l o g 4 n + 1 ) 1 − 3 16 + O ( n l o g 4 3 ) cn^2 + (\frac{3}{16})cn^2+(\frac{3}{16})^2cn^2+......+(\frac{3}{16})^{log_4^n-1}cn^2 + O(n^{log_4^3})=\frac{1\times (1-(\frac{3}{16})^{log_4^n+1})}{1-\frac{3}{16}}+O(n^{log_4^3}) cn2+(163)cn2+(163)2cn2+......+(163)log4n−1cn2+O(nlog43)=1−1631×(1−(163)log4n+1)+O(nlog43)

使用等比数列的上界作为上限：
c n 2 ∑ i = 0 l o g 4 n − 1 ( 3 16 ) i = c n 2 1 − 3 16 = 13 16 c n 2 cn^2\sum_{i=0}^{log_4^n-1}(\frac{3}{16})^i = \frac{cn^2}{1-\frac{3}{16}}=\frac{13}{16}cn^2 cn2i=0∑log4n−1(163)i=1−163cn2=1613cn2
所以：
T ( n ) = c n 2 + ( 3 16 ) c n 2 + ( 3 16 ) 2 c n 2 + . . . . . . + ( 3 16 ) l o g 4 n − 1 c n 2 + O ( n l o g 4 3 ) = 1 × ( 1 − ( 3 16 ) l o g 4 n + 1 ) 1 − 3 16 + O ( n l o g 4 3 ) ≤ 13 16 c n 2 + O ( n l o g 4 3 ) = O ( n 2 ) T(n) =cn^2 + (\frac{3}{16})cn^2+(\frac{3}{16})^2cn^2+......+(\frac{3}{16})^{log_4^n-1}cn^2 + O(n^{log_4^3})=\frac{1\times (1-(\frac{3}{16})^{log_4^n+1})}{1-\frac{3}{16}}+O(n^{log_4^3})\\ \leq \frac{13}{16}cn^2 +O(n^{log_4^3}) = O(n^2) T(n)=cn2+(163)cn2+(163)2cn2+......+(163)log4n−1cn2+O(nlog43)=1−1631×(1−(163)log4n+1)+O(nlog43)≤1613cn2+O(nlog43)=O(n2)

（2）迭代法证明

递归基础： T ( 1 ) = O ( 1 ) T(1) = O(1) T(1)=O(1)

归纳假设： T ( k ) ≤ c k 2 ，当 k < n 时成立 T(k) \leq ck^2，当k<n时成立 T(k)≤ck2，当k<n时成立

证明： T ( n ) ≤ c n 2 T(n) \leq cn^2 T(n)≤cn2
T ( n ) = 3 T ( n / 4 ) + d ( n 2 ) ≤ 3 c ( n / 4 ) 2 + d ( n 2 ) = 3 16 c n 2 + d ( n 2 ) ≤ c n 2 T(n) = 3T(n/4) + d(n^2)\\ \leq 3c(n/4)^2 + d(n^2)\\ =\frac{3}{16}cn^2 + d(n^2)\\ \leq cn^2 T(n)=3T(n/4)+d(n2)≤3c(n/4)2+d(n2)=163cn2+d(n2)≤cn2
当 d ≥ 16 13 c d\geq \frac{16}{13}c d≥1316c时成立。

4.3 Master Method

“cook book” Method for solving recurrences of the form:
T ( n ) = a T ( n / b ) + f ( n ) 其中 a ≥ 1 , b > 1 T(n) = aT(n/b) + f(n)\\ 其中a \geq 1 , b >1 T(n)=aT(n/b)+f(n)其中a≥1,b>1
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dfxG75kX-1654484649512)(…/…/…/…/Users/%E5%AD%99%E8%95%B4%E7%90%A6/AppData/Roaming/Typora/typora-user-images/image-20220606103409477.png)]

叶子的个数： a h = a l o g b n = n l o g b a a^h = a^{log_b^n} = n^{log_b^a} ah=alogbn=nlogba

比较树根 f ( n ) f(n) f(n)和 n l o g b a n^{log_b^a} nlogba

三种情况：
由根到叶子 { 减少不变增大由根到叶子\begin{cases}减少\\不变\\增大\end{cases} 由根到叶子⎩⎪⎨⎪⎧减少不变增大

4.3.1 Compare f(n) with n l o g b a n^{log_b^a} nlogba

（1） f ( n ) = O ( n l o g b a − ϵ ) f(n) = O(n^{log_{b}^{a}-\epsilon}) f(n)=O(nlogba−ϵ) 叶子开销严格大于树根

f ( n ) f(n) f(n)多项式增长慢于 n l o g b a ( b y a n n ϵ f a c t o r ) n^{log_b^a}(by\ an\ n^{\epsilon}\ factor) nlogba(by an nϵ factor)

S o l u t i o n : T ( n ) = Θ ( n l o g b a ) Solution:T(n) = \Theta(n^{log_b^a}) Solution:T(n)=Θ(nlogba)

注意是 Θ \Theta Θ

（2） f ( n ) = O ( n l o g b a ( l g n ) k ) f(n) = O(n^{log_{b}^{a}}(lgn)^k) f(n)=O(nlogba(lgn)k) 树根开销为叶子开销的 l g n lgn lgn的 k k k次方倍

其中 k ≥ 0 k\geq 0 k≥0，整数

S o l u t i o n : T ( n ) = Θ ( n l o g b a l g n k + 1 ) Solution:T(n) = \Theta(n^{log_b^a}lgn^{k+1}) Solution:T(n)=Θ(nlogbalgnk+1)最终结果多乘以一个树高的k次方

（3） f ( n ) = O ( n l o g b a + ϵ ) f(n) = O(n^{log_{b}^{a}+\epsilon}) f(n)=O(nlogba+ϵ) 叶子开销小于树根开销

需要额外满足 a f ( n / b ) ≤ c f ( n ) af(n/b)\leq cf(n) af(n/b)≤cf(n)

T ( n ) = Θ ( f ( n ) ) T(n)=\Theta(f(n)) T(n)=Θ(f(n))树根量级

4.3.2 Conclusion

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-syc8impv-1654484649512)(CH4%EF%BC%9ARecurrences.assets/image-20220606103532574.png)]

算法分析与设计CH4：Recurrences相关推荐

程振波算法设计与分析_算法分析与设计之动态规划
动态规划同样是一种将问题分解为求解子问题的方法,不过与分治不同的是,动态规划算法的子问题不是相互独立的,而是有公共的部分,即有重叠子问题,这个时候使用分治算法,将会重复计算公共的子问题,效率很低!而用 ...
一本好的教辅，可以少走很多弯路：算法分析和设计　王晓东
算法分析和设计王晓东我觉得第三版JAVA版本最好,第4版是C++版本,删减了几章. 可以配合北大屈婉玲教授的视频课程一起看自己走了一些弯路,希望后续的可以避免以下下载地址如下,也可以淘宝买本二 ...
非计算机专业教学改革,非计算机专业算法分析与设计教学改革论文
非计算机专业算法分析与设计教学改革论文 [摘要]算法分析与设计不仅是计算机专业的核心课程,同时也是与计算机有关的非计算机专业的专业课.本人针对非计算机专业学生在学习过程中存在的若干问题,就教学内容.教 ...
《算法分析与设计》课程任务
<算法分析与设计>课程任务内容包括以下8个部分,建议将任务按以下方式分解:其中1-6的每个部分的简介.适用条件.基本思想.基本步骤.复杂度分析等由1人讲解,实例分析由1人讲解(注:至少一 ...
用c语言验证装载问题回溯法,《算法分析与设计》期末考试复习题纲(完整版)...
<算法分析与设计>期末复习题一.选择题 1. 算法必须具备输入.输出和( D )等4个特性. A．可行性和安全性 B ．确定性和易读性 C．有穷性和安全性 D ．有穷性和确定性 2. ...
东师19年春计算机在线作业,东师算法分析与设计20春在线作业1【标准答案】
算法分析与设计20春在线作业1题目试卷总分:100 得分:100 一.单选题 (共 20 道试题,共 40 分) 1.按F5开始调试,程序便会直接运行到断点处.接下来可以逐行来运行程序,查看各个变 ...
算法分析与设计实验报告 ——二分搜索程序算法的实现
算法分析与设计实验报告 --二分搜索程序算法的实现实验目的及要求 1.理解分治算法的概念和基本要素: 2.理解递归的概念: 3.掌握设计有效算法的分治策略: 4.通过二分搜索技术学习分治策略设计技巧 ...
算法分析与设计实验报告——实现汽车加油问题
算法分析与设计实验报告--实现汽车加油问题目录: 算法分析与设计实验报告--实现汽车加油问题一. 实验目的二.实验要求三. 实验原理四. 实验过程(步骤) 五. 运行结果六.实验分析与讨论 ...
算法分析与设计实验报告——二分搜索算法的实现
算法分析与设计实验报告--二分搜索算法的实现目录: 算法分析与设计实验报告--二分搜索算法的实现一. 实验目的二.实验要求三. 实验原理四. 实验过程(步骤) 五. 运行结果六.实验分析与 ...

算法分析与设计CH4：Recurrences

CH4：Recurrences

4.1 Substitution Method 代换法

（1）步骤

（2）例子

Example1： T ( n ) = 4 T ( n / 2 ) + 100 n T(n) = 4T(n/2) + 100n T(n)=4T(n/2)+100n

Example2： T ( n ) = 2 T ( ⌊ n / 2 ⌋ ) + n T(n) = 2T(\lfloor n/2\rfloor) + n T(n)=2T(⌊n/2⌋)+n

Example3：尝试变量替换

（3）猜测方法

4.2 Recursion-tree Method

4.2.1 例子说明

（1）递归树猜测上界

（2）迭代法证明

4.3 Master Method

4.3.1 Compare f(n) with n l o g b a n^{log_b^a} nlogba

（1） f ( n ) = O ( n l o g b a − ϵ ) f(n) = O(n^{log_{b}^{a}-\epsilon}) f(n)=O(nlogba−ϵ) 叶子开销严格大于树根

（2） f ( n ) = O ( n l o g b a ( l g n ) k ) f(n) = O(n^{log_{b}^{a}}(lgn)^k) f(n)=O(nlogba(lgn)k) 树根开销为叶子开销的 l g n lgn lgn的 k k k次方倍

（3） f ( n ) = O ( n l o g b a + ϵ ) f(n) = O(n^{log_{b}^{a}+\epsilon}) f(n)=O(nlogba+ϵ) 叶子开销小于树根开销

4.3.2 Conclusion

算法分析与设计CH4：Recurrences相关推荐

最新文章

热门文章

算法分析与设计CH4：Recurrences

CH4：Recurrences

4.1 Substitution Method 代换法

（1）步骤

（2）例子

Example1： T ( n ) = 4 T ( n / 2 ) + 100 n T(n) = 4T(n/2) + 100n T(n)=4T(n/2)+100n

Example2： T ( n ) = 2 T ( ⌊ n / 2 ⌋ ) + n T(n) = 2T(\lfloor n/2\rfloor) + n T(n)=2T(⌊n/2⌋)+n

Example3：尝试变量替换

（3）猜测方法

4.2 Recursion-tree Method

4.2.1 例子说明

（1）递归树猜测上界

（2）迭代法证明

4.3 Master Method

4.3.1 Compare f(n) with n l o g b a n^{log_b^a} nlogba​

（1） f ( n ) = O ( n l o g b a − ϵ ) f(n) = O(n^{log_{b}^{a}-\epsilon}) f(n)=O(nlogba​−ϵ) 叶子开销严格大于树根

（2） f ( n ) = O ( n l o g b a ( l g n ) k ) f(n) = O(n^{log_{b}^{a}}(lgn)^k) f(n)=O(nlogba​(lgn)k) 树根开销为叶子开销的 l g n lgn lgn的 k k k次方倍

（3） f ( n ) = O ( n l o g b a + ϵ ) f(n) = O(n^{log_{b}^{a}+\epsilon}) f(n)=O(nlogba​+ϵ) 叶子开销小于树根开销

4.3.2 Conclusion

算法分析与设计CH4：Recurrences相关推荐

最新文章

热门文章

4.3.1 Compare f(n) with n l o g b a n^{log_b^a} nlogba

（1） f ( n ) = O ( n l o g b a − ϵ ) f(n) = O(n^{log_{b}^{a}-\epsilon}) f(n)=O(nlogba−ϵ) 叶子开销严格大于树根

（2） f ( n ) = O ( n l o g b a ( l g n ) k ) f(n) = O(n^{log_{b}^{a}}(lgn)^k) f(n)=O(nlogba(lgn)k) 树根开销为叶子开销的 l g n lgn lgn的 k k k次方倍

（3） f ( n ) = O ( n l o g b a + ϵ ) f(n) = O(n^{log_{b}^{a}+\epsilon}) f(n)=O(nlogba+ϵ) 叶子开销小于树根开销