傅里叶级数(离散谱)

[!] 以下笔记内容可能会出现部分错误的地方，恳请各位师生批评指正，谢谢！

主要内容

三角函数及正交性
傅里叶展开
频率谱与相位谱
傅里叶级数的复数形式

写在开头

由于目前我还是一名大一的学生，因此掌握的基础知识并不充足，部分内容无法用专业的术语来进行准确的概括，望谅解。
工程实际中有一大类型的函数 y = f ( t ) y=f(t) y=f(t)其自变量为时间，我们一般称之为时域信号。这些信号在时域上的轨迹常常表现的杂乱无章

若我们将这些信号转换到频域，提取它的频谱，就能很好地显现出特征来，这种方法成为频谱分析法，也是我要写的内容。

三角函数及正交性

1 三角函数

1.1 物理振动

在周期函数中，最简单的便是余弦函数 y = A c o s ( ω t + ϕ ) y=Acos(\omega t+\phi) y=Acos(ωt+ϕ)其中 A A A为振幅， ω \omega ω为角频率， ϕ \phi ϕ为初相。在物理中，满足这种运动规律的振动叫做简谐振动。确定了这三个变量，就能够唯一地确定一个三角函数。

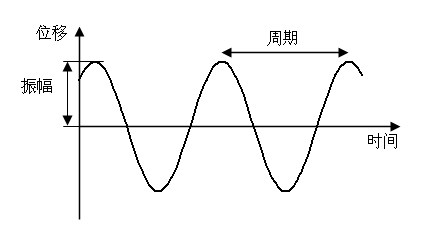
在物理中可知，振动具有叠加性，我们可以将任意一种复杂的周期振动看作是一系列简谐振动的合成。

1.2 电路分析

在非正弦周期电流电路上，激励信号源及电压电流响应都是不按照正弦规律变化的周期电路。为了分析这种电路，一般我们会使用到谐波分析法。
谐波分析法的实质就是将非正弦周期电流电路的计算转化为直流电路及一系列不同频率的正弦电流电路的计算。
一般的，对于电路中某种响应分量 f ( t ) f(t) f(t)，我们能够展开为 f ( t ) = A 0 + ∑ k = 1 ∞ A k m c o s ( k ω t + ϕ k ) f(t)=A_0+\sum^\infin_{k=1}A_{km}cos(k\omega t+\phi_k) f(t)=A0+k=1∑∞Akmcos(kωt+ϕk)其中常数项 A 0 A_0 A0称为 f ( t ) f(t) f(t)的直流分量， A 1 m c o s ( ω t + ϕ 1 ) A_{1m}cos(\omega t +\phi_1) A1mcos(ωt+ϕ1)称为一次谐波(又叫做基波)

1.3 三角函数系

不失一般性，我们可以得到：当满足某种条件的周期函数，能够分解为若干个三角函数的线性组合。为了更好地使用这种规律，首先我们需要知道为什么三角函数能够有这种效果。
在一个周期区间内，三角函数系具有如下性质
< sin ⁡ k ω t , cos ⁡ k ω t > = 0 < sin ⁡ k ω t , sin ⁡ n ω t > = 0 , ( n ≠ k ) < cos ⁡ k ω t , cos ⁡ n ω t > = 0 , ( n ≠ k ) <\sin{k\omega t},\cos{k\omega t}>=0\\ <\sin{k\omega t},\sin{n\omega t}>=0,(n\neq k)\\ <\cos{k\omega t},\cos{n\omega t}>=0,(n\neq k) <sinkωt,coskωt>=0<sinkωt,sinnωt>=0,(n=k)<coskωt,cosnωt>=0,(n=k)
这种性质我们称为正交性¹。
根据这种正交性，我们可以以此构建出一个特殊的坐标系 1 , cos ⁡ x , sin ⁡ x , cos ⁡ 2 x , sin ⁡ 2 x , … , cos ⁡ n x , sin ⁡ n x , … 1,\cos x,\sin x,\cos 2x,\sin 2x,\dots,\cos nx,\sin nx,\dots 1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx,…

该坐标系称为三角函数系。根据线性代数中提及到的内容能够得到，对于三角函数系中的坐标是线性无关的。
要注意的是，对于相同的两个三角函数的乘积积分在周期区间上不等于零 < sin ⁡ n ω x , sin ⁡ n ω x > = < cos ⁡ ω n x , cos ⁡ ω n x > = π ω = T 2 (1-1) <\sin n\omega x,\sin n\omega x>=<\cos \omega nx,\cos \omega nx>=\frac{\pi}{\omega}=\frac{T}{2}\tag{1-1} <sinnωx,sinnωx>=<cosωnx,cosωnx>=ωπ=2T(1-1)其中T为周期。

傅里叶展开

1 推导

我们现在有了一个三角函数系，在确定了 ω \omega ω的值之后，我们就可以张成一个空间。类比于机器学习中的样本空间(由样本不同的标签作为坐标轴)，其中的每一个样本都是样本空间中的一个数据点；因此根据物理和电工学中三角函数叠加的性质，在三角函数系中，每一个点都会对应着一个周期函数，用数学的方式来表达，即 f ( x ) = C + a 1 cos ⁡ ( ω x ) + b 1 s i n ( ω x ) + a 2 cos ⁡ ( 2 ω x ) + b 2 s i n ( 2 ω x ) + ⋯ + a n cos ⁡ ( n ω x ) + b n s i n ( n ω x ) + … f(x)=C+a_1\cos (\omega x)+b_1sin(\omega x)+\\a_2\cos (2\omega x)+b_2sin(2\omega x)+\dots+\\a_n\cos (n\omega x)+b_nsin(n\omega x)+\dots f(x)=C+a1cos(ωx)+b1sin(ωx)+a2cos(2ωx)+b2sin(2ωx)+⋯+ancos(nωx)+bnsin(nωx)+…
对于坐标轴 1 1 1可以看作是 n = 0 n=0 n=0时的情景的一半，即 C = a 0 cos ⁡ ( 0 ∗ ω x ) + b 0 sin ⁡ ( 0 ∗ ω x ) 2 = a 0 2 C=\frac{a_0\cos(0*\omega x)+b_0\sin(0*\omega x)}{2}=\frac{a_0}{2} C=2a0cos(0∗ωx)+b0sin(0∗ωx)=2a0因此代入并合并公式后，有 f ( x ) = a 0 2 + ∑ k = 1 ∞ [ a k cos ⁡ ( k ω x ) + b k sin ⁡ ( k ω x ) ] (2-1) f(x)=\frac{a_0}{2}+\sum^\infin_{k=1}[a_k\cos(k\omega x)+b_k\sin(k\omega x)]\tag{2-1} f(x)=2a0+k=1∑∞[akcos(kωx)+bksin(kωx)](2-1)这便是在三角函数系空间中任意一点的表达式
一般的周期函数 f ( t ) f(t) f(t)都能在 ω \omega ω相对应的三角函数系中找到相应的位置，也一一对应着一个展开公式(2-1)，这种展开叫做傅里叶展开，公式(2-1)称为傅里叶级数。

2 充分条件

并不是所有的周期函数都能有对应的傅里叶级数，在傅里叶展开中，需要满足以下条件的函数才能进行展开，这称为狄利克雷充分条件：
- 在一个周期内连续或只有有限个第一类间断点
- 在一个周期内至多只有有限个极值点
当满足狄利克雷充分条件后， f ( t ) f(t) f(t)的傅里叶级数收敛，并且有：
- 当 t t t是 f ( t ) f(t) f(t)的连续点时，级数收敛于 f ( t ) f(t) f(t)
- 当 t t t是 f ( t ) f(t) f(t)的间断点时，级数收敛于 1 2 [ f ( t − ) + f ( t + ) ] \frac{1}{2}[f(t^-)+f(t^+)] 21[f(t−)+f(t+)]
这个条件相比于泰勒展开条件(拥有任意阶导数)要低得多。
为了方便叙述，除非特别说明，否则后文中提到的周期函数都满足狄利克雷条件。

3 系数求解

现实中我们遇到的更多是给定一个周期函数，然后求解出它的傅里叶级数。为此，我们需要找出一种方法来得到一系列的变量 a 0 、 a n 、 b n , ( n = 1 , 2 , … ) a_0、a_n、b_n,(n=1,2,\dots) a0、an、bn,(n=1,2,…)
按照线性代数的思想，我们可以使用投影的方式来得到坐标系的一系列变量，将向量与基向量做点乘，即可得到对应于该基向量坐标轴的值。
对于三角函数系也同样适用，即 a k = < f ( t ) , cos ⁡ k ω t > = 2 T ∫ − T 2 T 2 f ( t ) cos ⁡ ( k ω t ) d t , ( k = 0 , 1 , 2 , … ) a_k=<f(t),\cos k\omega t>=\frac{2}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}f(t)\cos(k\omega t)dt,(k=0,1,2,\dots) ak=<f(t),coskωt>=T2∫−2T2Tf(t)cos(kωt)dt,(k=0,1,2,…) b n = < f ( t ) , sin ⁡ k ω t > = 2 T ∫ − T 2 T 2 f ( t ) sin ⁡ ( k ω t ) d t , ( n = 1 , 2 , … ) b_n=<f(t),\sin k\omega t>=\frac{2}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}f(t)\sin(k\omega t)dt,(n=1,2,\dots) bn=<f(t),sinkωt>=T2∫−2T2Tf(t)sin(kωt)dt,(n=1,2,…)

4 正弦级数与余弦级数

对于一般的傅里叶级数既含有正弦项也含有余弦项，但根据三角函数的一些性质，我们可以将其中的正弦项或余弦项去掉。
由于奇函数在对称区间上的积分为零，因此根据傅里叶级数的系数求解公式可以得到：奇函数的傅里叶展开公式中不存在余弦项，此时级数中只有正弦项。因此奇函数的傅里叶级数又称为正弦级数，即 f ( x ) = ∑ n = 1 ∞ b n sin ⁡ n ω x f(x)=\sum^\infin_{n=1}b_n\sin n\omega x f(x)=n=1∑∞bnsinnωx
同理，偶函数的傅里叶展开公式中不存在正弦项，因此偶函数的傅里叶级数又称为余弦级数，有 f ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n ω x f(x)=\frac{a_0}{2}+\sum^\infin_{n=1}a_n\cos n\omega x f(x)=2a0+n=1∑∞ancosnωx

5 电工学表示

在电工学中，为了更好地表示电路中的参数，我们都会将傅里叶级数转换成如下形式： f ( t ) = A 0 + ∑ k = 1 ∞ A k m c o s ( k ω t + ϕ k ) f(t)=A_0+\sum^\infin_{k=1}A_{km}cos(k\omega t+\phi_k) f(t)=A0+k=1∑∞Akmcos(kωt+ϕk)其中展开式的参数由以下式子确定：
A 0 = a 0 2 , A k m = a k 2 + b k 2 , ( k = 1 , 2 , … ) A_0=\frac{a_0}{2},A_{km}=\sqrt{a_k^2+b_k^2},(k=1,2,\dots) A0=2a0,Akm=ak2+bk2 ,(k=1,2,…)
ϕ k = − arctan ⁡ b k a k , ( k = 1 , 2 , … ) \phi_k=-\arctan\frac{b_k}{a_k},(k=1,2,\dots) ϕk=−arctanakbk,(k=1,2,…)

幅值频谱与相位频谱

1 时域与频域

在对函数或信号进行分析时通常分为分为两个部分：时间和频率。根据分析部分的不同我们划分了时域与频域两个概念。
时域中的函数能够直观地表达出信号在时间下的变化规律；而频域中的函数能够直观地表达出信号不同频率的信息。
对于周期函数，我们可以通过傅里叶级数来完成从时域到频域的转换。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iWt22GYL-1592556352687)(https://upload.wikimedia.org/wikipedia/commons/4/4f/Triangle-td_and_fd.png)]
[上图部分为时域图像，下图则为频域图像，两者表达的是同一个周期函数]

2 幅值频谱

当我们以频率 ω \omega ω为横轴，振幅 A A A为纵轴时对函数的傅里叶级数作图，即可得到幅值频谱。
由于傅里叶级数中的振幅 A k m A_{km} Akm中只在 ω \omega ω的整数倍时有值，因此在幅值频谱也称为离散幅值频谱。而 ω \omega ω也称为基频。在理想情况下，幅值频谱是由若干个狄拉克 δ \delta δ函数的线性组合组成。²

3 相位频谱

当我们以频率 ω \omega ω为横轴，初相 ϕ \phi ϕ为纵轴时作图，即可得到相位频谱。
与幅值频谱相同，由于傅里叶级数中的初相 ϕ k \phi_k ϕk也是离散的，因此在理想情况下，相位频谱也是由若干个狄拉克 δ \delta δ函数的线性组合组成。

傅里叶级数的复数形式

为了将周期函数的傅里叶展开拓展到非周期函数上，我们首先需要先得到另一种更好的描述方式，即傅里叶级数的复数形式。

1 欧拉公式

用于将三角函数用复数形式展示的桥梁为欧拉公式。欧拉公式提出，对于任意实数 x x x，都存在 e i π = cos ⁡ x + i sin ⁡ x e^{i\pi}=\cos x+i\sin x eiπ=cosx+isinx其中 e e e 是自然对数的底数，而 i i i 是虚数单位。
根据欧拉公式，我们能够得到 cos ⁡ n ω t = e i n ω t + e − i n ω t 2 \cos n\omega t=\frac{e^{in\omega t}+e^{-in\omega t}}{2} cosnωt=2einωt+e−inωt sin ⁡ n ω t = e i n ω t − e − i n ω t 2 \sin n \omega t=\frac{e^{in\omega t}-e^{-in\omega t}}{2} sinnωt=2einωt−e−inωt

2 傅里叶级数的复数形式

代入傅里叶级数的展开式，有 f ( t ) = a 0 2 + ∑ n = 1 ∞ [ a n 2 ( e i n ω t + e − i n ω t ) − i b n 2 ( e i n ω t − e − i n ω t ) ] = a 0 2 + ∑ n = 1 n ( a n − i b n 2 e i n ω t + a n + i b n 2 e − i n ω t ) f(t)=\frac{a_0}{2}+\sum^\infin_{n=1}[\frac{a_n}{2}(e^{in\omega t}+e^{-in\omega t})-\frac{ib_n}{2}(e^{in\omega t}-e^{-in\omega t})]\\=\frac{a_0}{2}+\sum^n_{n=1}(\frac{a_n-ib_n}{2}e^{in\omega t}+\frac{a_n+ib_n}{2}e^{-in\omega t}) f(t)=2a0+n=1∑∞[2an(einωt+e−inωt)−2ibn(einωt−e−inωt)]=2a0+n=1∑n(2an−ibneinωt+2an+ibne−inωt)
令 c 0 = a 0 2 c_0=\frac{a_0}{2} c0=2a0 c n = a n − i b n 2 = 1 T ∫ T 2 T 2 f ( t ) e − i n ω t d t c_n=\frac{a_n-ib_n}{2}=\frac{1}{T}\int^{\frac{T}{2}}_{\frac{T}{2}}f(t)e^{-in\omega t}dt cn=2an−ibn=T1∫2T2Tf(t)e−inωtdt c − n = a n + i b n 2 = 1 T ∫ T 2 T 2 f ( t ) e i n ω t d t c_{-n}=\frac{a_n+ib_n}{2}=\frac{1}{T}\int^{\frac{T}{2}}_{\frac{T}{2}}f(t)e^{in\omega t}dt c−n=2an+ibn=T1∫2T2Tf(t)einωtdt³
代入后，可以得到简化的形式 f ( t ) = ∑ n = 1 ∞ c − n e − i n ω t + c 0 + ∑ n = 1 ∞ c n e i n ω t f(t)=\sum^\infin_{n=1}c_{-n}e^{-in\omega t}+c_0+\sum^\infin_{n=1}c_{n}e^{in\omega t} f(t)=n=1∑∞c−ne−inωt+c0+n=1∑∞cneinωt进一步化简，有 f ( t ) = ∑ n = − ∞ ∞ c n e i n ω t , n = 0 , ± 1 , ± 2 , ⋯ f(t)=\sum^\infin_{n=-\infin}c_ne^{in\omega t},n=0,±1,±2,\cdots f(t)=n=−∞∑∞cneinωt,n=0,±1,±2,⋯

参考

[1]Wiki.简谐振动[EB/OL].https://zh.wikipedia.org/wiki/简谐运动.
[2]章云.微积分理论与实践[M].机械工业出版社:北京,2019:315-324.
[3]同济大学数学系.高等数学第七版(下册)[M].高等教育出版社:北京,2014.
[4]范仰才.大学物理学(上).北京大学出版社:北京,2018.
[5]林珊.电路.机械工业出版社:北京,2016.
[6]Wiki.狄利克雷定理(傅里叶级数)[EB/OL].https://zh.wikipedia.org/wiki/狄利克雷定理(傅里叶级数).
[7]Wiki.频域[EB/OL].https://zh.wikipedia.org/wiki/频域.

这种是函数意义上的正交，可以理解为在某种特定情况下的一种垂直。 ↩︎
实际操作中这个函数是通过傅里叶变换获得的，因此也会存在着局部连续的情况。 ↩︎
这里的 c n c_n cn和 c − n c_{-n} c−n中的积分形式使用了定积分的线性组合性质，将 a n a_n an和 b n b_n bn的积分进行线性组合后用欧拉公式转为指数形式。 ↩︎

谱分析——傅里叶级数(离散谱)相关推荐

matlab fft谱分析实验报告,基于matlab的fft频谱分析及应用实验报告.docx
基于matlab的fft频谱分析及应用实验报告实验三用FFT对信号进行频谱分析一实验目的 1能够熟练掌握快速离散傅立叶变换的原理及应用FFT进行频谱分析的基本方法:2了解用FFT进行频谱分析可能出 ...
dft计算傅里叶级数系数_一道国外的DFT性质的题目
由于上半年实在太忙太忙,所以导致很久没更新公众号了,特意向各位长期关注的小伙伴表示歉意.今天分享的是DFT性质的应用. 背景:DFT的对称性在解题中是非常常见的,很多同学,一看到"实序列&q ...
matlab求傅里叶级数展开式_傅里叶级数：从向量的角度看函数
帮助你理解线性代数与机器学习紧密结合的核心内容下文节选自北大出版社<机器学习线性代数基础>, [遇见]已获授权许可. 这本书不同于传统教材, 从新的角度来介绍线性代数的核心知识, 讲解也 ...
随机过程基础3--宽平稳随机过程的谱分析
本节关于随机过程的谱分析,当然是针对宽平稳随机过程 1,什么是谱? 将复杂对象分解成几个方面,使得我们可以从几个方面尽可能简单地观察这个复杂对象的某些特征. 例如光谱是按照光的波长分解. 对于随机信号 ...
傅里叶级数及傅里叶变换
通信中的信号通常是时间的函数. 下面通过强度.频率.相位.能量来了解信号(正如通过人的五官去了解人): 正弦信号: 周期信号的傅里叶级数: 用正弦信号逼近方波: 如下图:船的振荡频率为 ,跷跷板的频率 ...
高等数学——傅里叶级数
扩展来自一位学长: 傅里叶级数选择三角函数集,只是因为三角函数集一类特殊的正交函数集,其实还有很多其他的正交函数集.以下是学长附的图(我也没太看懂): 其实,我们完全可以用其他的完备正交函数集来拟合 ...
数字信号处理（9）- 模拟信号的谱分析方法
1 用DFT对模拟信号进行频谱分析引入: DFT的最初引入就是为了使数字计算机能够帮助分析连续时间信号的频谱 DFT的快速算法(FFT)的出现使得DFT这种分析方法具有实用价值和重要性. DFT即发 ...
对傅里叶级数和傅里叶变换的理解
前言以前学信号.高数.复变函数接触过傅里叶级数和傅里叶变换,现在整理一下目前自己对傅里叶级数.傅立叶变换浅薄的理解,本文参考了李永乐老师的科普和一些知乎上的文章,如有冒犯之处请联系我.如有错误的地方 ...
Python - SciPy - ECG信号的谱分析及数字滤波
本节的阅读需要傅里叶级数及傅里叶变换的相关数学知识. 示范代码目录下有一个ecgsignal.dat文件,这里存储了作者采集的一段人体心电信号-ECG.这个文件以4字节浮点数存储样本,单位为μV,采样 ...

谱分析——傅里叶级数(离散谱)