[Luogu P3288] [BZOJ 3597] [SCOI2014]方伯伯运椰子

题目描述

四川的方伯伯为了致富，决定引进海南的椰子树。方伯伯的椰子园十分现代化，椰子园中有一套独特的交通系统。

现在用点来表示交通节点，边来表示道路。这样，方伯伯的椰子园就可以看作一个有 n + 2 个交通节点，m条边的有向无环图。 n + 1 n +1 n+1 号点为入口， n + 2 n+2 n+2 号点为出口。每条道路都有 6 6 6 个参数， u i u_i ui， v i v_i vi， a i a_i ai， b i b_i bi， c i c_i ci， d i d_i di，分别表示，该道路从 u i u_i ui 号点通向 v i v_i vi 号点，将它的容量压缩一次要 a i a_i ai 的花费，容量扩大一次要 b i b_i bi 的花费，该条道路当前的运输容量上限为 c i c_i ci，并且每单位运输量通过该道路要 d i d_i di 的费用。

在这个交通网络中，只有一条道路与起点相连。因为弄坏了这条道路就会导致整个交通网络瘫痪，聪明的方伯伯决定绝不对这条道路进行调整，也就是说，现在除了这条道路之外，对其余道路都可以进行调整。

有两种调整方式：

选择一条道路，将其进行一次压缩，这条道路的容量会下降 1 1 1 单位。
选择一条道路，将其进行一次扩容，这条道路的容量会上升 1 1 1 单位。

一条道路可以被多次调整。

由于很久以前，方伯伯就请过一个工程师，对这个交通网络进行过一次大的优化调整。所以现在所有的道路都被完全的利用起来了，即每条道路的负荷都是满的（每条道路的流量等于其容量）。

但方伯伯一想到自己的海南椰子会大丰收，就十分担心巨大的运输量下，会导致过多的花费。因此，方伯伯决定至少进行一次调整，调整之后，必须要保持每条道路满负荷，且总交通量不会减少。

设调整后的总费用是 Y Y Y，调整之前的总费用是 X X X。现在方伯伯想知道，最优调整比率是多少，即假设他进行了 k k k 次调整， X − Y k \frac{X - Y}{k} kX−Y最大能是多少？

注：总费用 = = = 交通网络的运输花费 + 调整的花费

输入输出格式

输入格式：

第一行包含二个整数 N N N， M M M接下来 M M M行代表 M M M条边，表示这个交通网络每行六个整数，表示 U i , V i , A i , B i , C i , D i U_i,V_i,A_i,B_i,C_i,D_i Ui,Vi,Ai,Bi,Ci,Di接下来一行包含一条边，表示连接起点的边

输出格式：

一个浮点数，保留二位小数。表示答案，数据保证答案大于 0 0 0

输入输出样例

输入样例#1：

5 10
1 5 13 13 0 412
2 5 30 18 396 148
1 5 33 31 0 39
4 5 22 4 0 786
4 5 13 32 0 561
4 5 3 48 0 460
2 5 32 47 604 258
5 7 44 37 75 164
5 7 34 50 925 441
6 2 26 38 1000 22

输出样例#1：

103.00

说明

1 ≤ N ≤ 5000 , 0 ≤ M ≤ 3000 , 1 ≤ U i , V i ≤ N + 2 , 0 ≤ A i , B i ≤ 500 , 0 ≤ C i ≤ 10000 , 0 ≤ D i ≤ 1000 1\leq N\leq 5000, 0\leq M\leq 3000, 1\leq Ui,Vi\leq N+2, 0\leq Ai,Bi\leq 500, 0\leq Ci\leq 10000, 0\leq Di\leq 1000 1≤N≤5000,0≤M≤3000,1≤Ui,Vi≤N+2,0≤Ai,Bi≤500,0≤Ci≤10000,0≤Di≤1000

解题分析

看题目所求，显然是一道分数规划，然而我们应该如何构图？

假设原来 D A G DAG DAG的一部分是这个样子的：

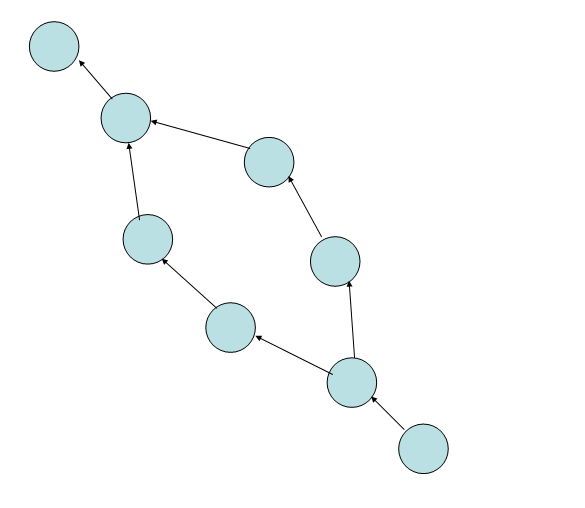
如果我们要将一部分道路的流量缩小（例如上图靠左的一半路径），并保证所有边仍然满流，那么肯定会将这些路径的流量都 − 1 -1 −1，其他部分的边的流量 + 1 +1 +1。具体而言会变成这样：

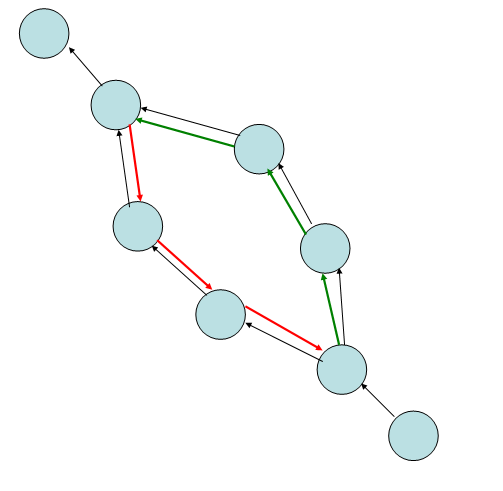
显然就形成了一个环。那么我们单位流量沿着红色边走的代价就是 a − d a-d a−d（因为相当于减少了流量），沿着绿色边走的代价就是 b + d b+d b+d。

我们设 a n s = m a x { X − Y k } ans=max\{\frac{X-Y}{k} \} ans=max{kX−Y}，那么对于图中的任何一个环都有 a n s × k ≥ X − Y ans\times k\ge X-Y ans×k≥X−Y（在这里 X − Y X-Y X−Y就是如上图所示环中原来的边与红色边和绿色边代价和的差）。因为我们是求一个最值，所以我们只需要关心单位流量的情况，即只要 c ≠ 0 c\neq 0 c̸=0即可从 v v v向 u u u连边。

考虑如何将 a n s × k ans\times k ans×k带入计算。我们发现环中其实就有 k k k个点，那么二分 a n s ans ans，把对应的边权加上 a n s ans ans就好。如果跑 S P F A SPFA SPFA时仍然有负环，那么仍然满足要求，可以提升二分下界，否则降低上界。

另外，注意图中共有 n + 2 n+2 n+2个点！否则会 W A WA WA到天边…

代码如下：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <cctype>
#include <cmath>
#define R register
#define IN inline
#define W while
#define gc getchar()
#define MX 5050
#define db double
#define ll long long
#define EPS 1e-3
template <class T>
IN void in(T &x)
{x = 0; R char c = gc;for (; !isdigit(c); c = gc);for (;  isdigit(c); c = gc)x = (x << 1) + (x << 3) + c - 48;
}
int dot, line, cnt;
int head[MX];
db dis[MX];
bool vis[MX];
struct Edge {int to, len, nex;} edge[MX << 3];
IN void add(R int from, R int to, R int len)
{edge[++cnt] = {to, len, head[from]}, head[from] = cnt;}
bool SPFA(R int now, db tar)
{vis[now] = true;for (R int i = head[now]; i; i = edge[i].nex){if(dis[edge[i].to] > dis[now] + edge[i].len + tar){dis[edge[i].to] = dis[now] + edge[i].len + tar;if(vis[edge[i].to]) return true;if(SPFA(edge[i].to, tar)) return vis[now] = false, true;}}return vis[now] = false;
}
IN bool check(db tar)
{std::memset(vis, false, sizeof(vis));std::memset(dis, 0, sizeof(dis));for (R int i = 1; i <= dot; ++i)if(SPFA(i, tar)) return true;return false;
}
IN void solve()
{db lef = 0, rig = 1e8, mid;W(rig - lef > EPS){mid = (lef + rig) / 2;if(check(mid)) lef = mid;else rig = mid;}printf("%.2lf", mid);
}
int main(void)
{int u, v, a, b, c, d;in(dot), in(line); dot += 2;for (R int i = 1; i <= line; ++i){in(u), in(v), in(a), in(b), in(c), in(d);if(c) add(v, u, a - d);add(u, v, b + d);}solve();
}