信息熵、联合熵、条件熵、互信息

1. 自信息量

一个随机事件xxx的自信息量¹定义为：
I(x)=log⁡1p(x)I(x)=\log\frac{1}{p(x)}I(x)=logp(x)1

注意，在信息论中，log⁡\loglog函数的底通常设置为2，此时，自信息量的单位为比特(bit)；在机器学习中，log⁡\loglog函数的底通常设置为自然常数e，此时，自信息量的单位为奈特(nat)。

需要从以下两方面来理解自信息量：

自信息量表示，如果随机事件xxx发生的概率p(x)p(x)p(x)越小，一旦其发生，所获得的信息量就越大
自信息量反映了事件发生的不确定性

举例说明，“中彩票”事件的概率极小，但是一旦中了彩票，“中彩票”事件的自信息量很大，也就是说，“中彩票”会获得极大的信息量（即收益）。另一方面，“中彩票”事件的概率很低，自信息量很大，意味着“中彩票”事件发生的不确定性也很大。

发生概率越高的事情，具有的自信息量越少

发生概率越低的事情，具有的自信息量越多

2. 信息熵

一个随机变量XXX的信息熵²定义为：
H(X)=∑xi∈Xp(xi)I(xi)=∑xi∈Xp(xi)log⁡1p(xi).H(X) = \sum_{x_i\in X}p(x_i)I(x_i)\\ = \sum_{x_i\in X}p(x_i)\log\frac{1}{p(x_i)}. H(X)=xi∈X∑p(xi)I(xi)=xi∈X∑p(xi)logp(xi)1.

简记为：H(X)=−∑xp(x)log⁡p(x).H(X)=-\sum_{x}p(x)\log p(x).H(X)=−x∑p(x)logp(x).

信息熵的单位与自信息量一样。一个随机变量XXX可以有多种取值可能，信息熵是随机变量XXX所有可能情况的自信息量的期望。信息熵H(X)H(X)H(X)表征了随机变量XXX所有情况下的平均不确定度。

不确定度越大，信息量越大

不确定度越小，信息量越小

3. 最大熵定理

当随机变量XXX所有取值的概率相等时，即p(xi)p(x_i)p(xi)的概率都相等时，信息熵取最大值，随机变量具有最大的不确定性。例如，情景一：买彩票中奖和不中奖的概率都是0.50.50.5时，此时买彩票是否中奖的不确定性最大。情景二：真实情况中，不中奖的概率远远大于中奖的概率，此时的不确定性要小于情景一，因为几乎能确定为不中奖。

最大熵定理: 当随机变量XXX，在离散情况下所有取值概率相等（或在连续情况下服从均匀分布），此时熵最大。即0≤H(X)≤log⁡∣X∣0\leq H(X)\leq \log |X|0≤H(X)≤log∣X∣，其中∣X∣|X|∣X∣表示XXX的取值个数。

例1. 根据经验判断，买彩票中奖的概率是80%80\%80%，不中奖的概率是20%20\%20%，求买彩票的信息熵。

解：买彩票的概率空间为：
(XP)=(x1x20.80.2)\binom{X}{P}=\begin{pmatrix} x_{1} &x_{2} \\ 0.8 & 0.2 \end{pmatrix}(PX)=(x10.8x20.2)

其中，x1x_{1}x1表示买的彩票没奖，x2x_{2}x2表示买的彩票有奖。

买彩票后，“没中奖”事件获得的自信息量为：
I(x1)=log⁡210.8=log⁡21.25=log⁡101.25log⁡102=0.322bitI(x_1)=\log_2\frac{1}{0.8}=\log_21.25=\frac{\log_{10}1.25}{\log_{10}2}=0.322~\text{bit}I(x1)=log20.81=log21.25=log102log101.25=0.322 bit
买彩票后，“中奖”事件获得的自信息量为：
I(x2)=log⁡210.2=log⁡25=log⁡105log⁡102=2.322bitI(x_2)=\log_2\frac{1}{0.2}=\log_25=\frac{\log_{10}5}{\log_{10}2}=2.322~\text{bit}I(x2)=log20.21=log25=log102log105=2.322 bit

由I(x1)<I(x2)I(x_1)<I(x_2)I(x1)<I(x2)可知，彩票有奖的不确定性要大于彩票没奖。

买彩票的信息熵为：
H(X)=p(x1)I(x1)+p(x2)I(x2)=0.8∗0.322+0.2∗2.322=0.722bitH(X)=p(x_1)I(x_1)+p(x_2)I(x_2)=0.8*0.322+0.2*2.322=0.722~\text{bit}H(X)=p(x1)I(x1)+p(x2)I(x2)=0.8∗0.322+0.2∗2.322=0.722 bit

**结果分析：**由最大熵定理可知，信息熵H(X)H(X)H(X)的最大值为H(X)max⁡=−log⁡1/2=1H(X)_{\max}=-\log 1/2=1H(X)max=−log1/2=1。例111中H(X)H(X)H(X)小于1比特，意味着不确定性减少，带来的信息量也减少。也就是说，先验经验（买彩票大概率不中奖）减少了不确定性。

4. 联合熵

随机变量XXX和YYY的联合熵定义为：
H(X,Y)=∑xi∈X∑yi∈Yp(xi,yi)I(xi,yi)=∑xi∈X∑yi∈Yp(xi,yi)log1p(xi,yi)H(X, Y)=\sum_{x_i\in X}\sum_{y_i\in Y}p(x_i, y_i)I(x_i, y_i)\\ =\sum_{x_i\in X}\sum_{y_i\in Y}p(x_i, y_i)log\frac{1}{p(x_i, y_i)} H(X,Y)=xi∈X∑yi∈Y∑p(xi,yi)I(xi,yi)=xi∈X∑yi∈Y∑p(xi,yi)logp(xi,yi)1

简记为：H(X,Y)=−∑x,yp(x,y)log⁡p(x,y)H(X, Y)=-\sum_{x,y}p(x,y)\log p(x,y)H(X,Y)=−x,y∑p(x,y)logp(x,y)

**联合熵H(X,Y)H(X, Y)H(X,Y)表示随机变量XXX和YYY一起发生时的信息熵，即XXX和YYY一起发生时的确定度。**通俗地讲，联合熵H(X,Y)H(X, Y)H(X,Y)表示XXX和YYY一起发生时，产生的信息量。

5. 条件熵H(X∣Y)H(X|Y)H(X∣Y)

随机变量XXX和YYY的**条件熵H(Y∣X)H(Y|X)H(Y∣X)**定义为：
H(X∣Y)=∑yj∈Yp(yj)H(X∣Y=yj)H(X|Y)=\sum_{y_j\in Y}p(y_j)H(X|Y=y_j)H(X∣Y)=yj∈Y∑p(yj)H(X∣Y=yj)

**条件熵H(X∣Y)H(X|Y)H(X∣Y)表示已知随机变量YYY的情况下，随机变量XXX的信息熵，即在YYY发生的前提下，XXX发生后新带来的不确定度。**通俗地讲，条件熵H(X∣Y)H(X|Y)H(X∣Y)表示在YYY发生的前提下，XXX发生新带来的信息量。

具体使用形式为：
H(X∣Y)=∑yj∈Yp(yj)H(X∣Y=yj)=−∑yj∈Yp(yj)∑xi∈Xp(xi∣yj)log⁡p(xi∣yj)=−∑yj∈Y∑xi∈Xp(yj)p(xi∣yj)log⁡p(xi∣yj)=−∑xi,yjp(xi,yj)log⁡p(xi∣yj)H(X|Y) = \sum_{y_j\in Y}p(y_j)H(X|Y=y_j) \\ = -\sum_{y_j\in Y}p(y_j)\sum_{x_i\in X}p(x_i|y_j)\log p(x_i|y_j)\\ = -\sum_{y_j\in Y}\sum_{x_i\in X}p(y_j)p(x_i|y_j)\log p(x_i|y_j)\\ = -\sum_{x_i,y_j}p(x_i,y_j)\log p(x_i|y_j) H(X∣Y)=yj∈Y∑p(yj)H(X∣Y=yj)=−yj∈Y∑p(yj)xi∈X∑p(xi∣yj)logp(xi∣yj)=−yj∈Y∑xi∈X∑p(yj)p(xi∣yj)logp(xi∣yj)=−xi,yj∑p(xi,yj)logp(xi∣yj)

简记为：H(X∣Y)=−∑x,yp(x,y)log⁡p(x∣y)H(X|Y)=-\sum_{x,y}p(x,y)\log p(x|y)H(X∣Y)=−x,y∑p(x,y)logp(x∣y)

条件熵H(X∣Y)H(X|Y)H(X∣Y)与联合熵H(X,Y)H(X,Y)H(X,Y)的关系为：
H(X∣Y)=H(X,Y)−H(Y)H(X|Y)=H(X,Y)-H(Y)H(X∣Y)=H(X,Y)−H(Y)

推导过程如下：
H(X∣Y)=−∑x,yp(x,y)log⁡p(x∣y)=−∑x,yp(x,y)log⁡p(x,y)p(y)=−∑x,yp(x,y)log⁡p(x,y)+∑x,yp(x,y)log⁡p(y)=−∑x,yp(x,y)log⁡p(x,y)+∑y（∑xp(x,y)）log⁡p(y)=−∑x,yp(x,y)log⁡p(x,y)+∑yp(y)log⁡p(y)=H(X,Y)−H(Y)H(X|Y) = -\sum_{x,y}p(x,y)\log p(x|y)\\ = -\sum_{x,y}p(x,y)\log \frac{p(x,y)}{p(y)}\\ = -\sum_{x,y}p(x,y)\log p(x,y)+\sum_{x,y}p(x,y)\log p(y)\\ = -\sum_{x,y}p(x,y)\log p(x,y)+\sum_{y}（\sum_{x}p(x,y)）\log p(y)\\ = -\sum_{x,y}p(x,y)\log p(x,y)+\sum_{y}p(y)\log p(y)\\ = H(X,Y)-H(Y) H(X∣Y)=−x,y∑p(x,y)logp(x∣y)=−x,y∑p(x,y)logp(y)p(x,y)=−x,y∑p(x,y)logp(x,y)+x,y∑p(x,y)logp(y)=−x,y∑p(x,y)logp(x,y)+y∑（x∑p(x,y)）logp(y)=−x,y∑p(x,y)logp(x,y)+y∑p(y)logp(y)=H(X,Y)−H(Y)

5. 条件熵H(Y∣X)H(Y|X)H(Y∣X)

随机变量XXX和YYY的**条件熵H(Y∣X)H(Y|X)H(Y∣X)**定义为：
H(Y∣X)=∑xi∈Xp(xi)H(Y∣X=xi)H(Y|X)=\sum_{x_i\in X}p(x_i)H(Y|X=x_i)H(Y∣X)=xi∈X∑p(xi)H(Y∣X=xi)

**条件熵H(Y∣X)H(Y|X)H(Y∣X)表示已知随机变量XXX的情况下，随机变量YYY的信息熵，即在XXX发生的前提下，YYY发生后新带来的不确定度。**通俗地讲，条件熵H(Y∣X)H(Y|X)H(Y∣X)表示在XXX发生的前提下，YYY发生新带来的信息量。

具体使用形式为：
H(Y∣X)=∑xi∈Xp(xi)H(Y∣X=xi)=−∑xi∈Xp(xi)∑yj∈Yp(yj∣xi)log⁡p(yj∣xi)=−∑xi∈X∑yj∈Yp(xi)p(yj∣xi)log⁡p(yj∣xi)=−∑xi,yjp(xi,yj)log⁡p(yj∣xi)H(Y|X) = \sum_{x_i\in X}p(x_i)H(Y|X=x_i) \\= -\sum_{x_i\in X}p(x_i)\sum_{y_j\in Y}p(y_j|x_i)\log p(y_j|x_i)\\ = -\sum_{x_i\in X}\sum_{y_j\in Y}p(x_i)p(y_j|x_i)\log p(y_j|x_i)\\ = -\sum_{x_i,y_j}p(x_i,y_j)\log p(y_j|x_i) H(Y∣X)=xi∈X∑p(xi)H(Y∣X=xi)=−xi∈X∑p(xi)yj∈Y∑p(yj∣xi)logp(yj∣xi)=−xi∈X∑yj∈Y∑p(xi)p(yj∣xi)logp(yj∣xi)=−xi,yj∑p(xi,yj)logp(yj∣xi)

简记为：H(Y∣X)=−∑x,yp(x,y)log⁡p(y∣x)H(Y|X)=-\sum_{x,y}p(x,y)\log p(y|x)H(Y∣X)=−x,y∑p(x,y)logp(y∣x)

条件熵H(Y∣X)H(Y|X)H(Y∣X)与联合熵H(X,Y)H(X,Y)H(X,Y)的关系为：
H(Y∣X)=H(X,Y)−H(X)H(Y|X)=H(X,Y)-H(X)H(Y∣X)=H(X,Y)−H(X)

推导过程见H(X∣Y)H(X|Y)H(X∣Y)。

7. 互信息

互信息量定义为后验概率与先验概率比值的对数：
I(xi;yj)=log⁡p(xi∣yj)p(xi)I(x_i;y_j)=\log \frac{p(x_i|y_j)}{p(x_i)}I(xi;yj)=logp(xi)p(xi∣yj)

互信息（平均互信息量）：
I(X;Y)=∑xi∈X∑yj∈Yp(xi,yj)log⁡p(xi∣yj)p(xi)I(X;Y)=\sum_{x_i\in X}\sum_{y_j \in Y}p(x_i,y_j)\log \frac{p(x_i|y_j)}{p(x_i)}I(X;Y)=xi∈X∑yj∈Y∑p(xi,yj)logp(xi)p(xi∣yj)

简记为：
I(X;Y)=∑x,yp(x,y)log⁡p(x∣y)p(x)I(X;Y)=\sum_{x,y}p(x,y)\log \frac{p(x|y)}{p(x)}I(X;Y)=x,y∑p(x,y)logp(x)p(x∣y)

互信息具有以下性质：
I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=I(Y;X)I(X;Y) = H(X)-H(X|Y) = H(Y)-H(Y|X) = I(Y;X) I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=I(Y;X)

互信息的理解：
H(X)H(X)H(X)是XXX的不确定度，H(X∣Y)H(X|Y)H(X∣Y)是YYY已知时是XXX的不确定度，则I(X;Y)=H(X)−H(X∣Y)I(X;Y)=H(X)-H(X|Y)I(X;Y)=H(X)−H(X∣Y)表示YYY已知使得XXX的不确定度减少了I(X;Y)I(X;Y)I(X;Y)。YYY已知时XXX的不确定度为H(X∣Y)=H(X)−I(X;Y)H(X|Y)=H(X)-I(X;Y)H(X∣Y)=H(X)−I(X;Y)。

8. 小结

名称	公式	含义
熵H(X)H(X)H(X)	H(X)=−∑x∈Xp(x)log⁡p(x)H(X)=-\sum_{x\in X}p(x)\log p(x)H(X)=−∑x∈Xp(x)logp(x)	熵H(X)H(X)H(X)表示XXX的不确定度
联合熵H(X,Y)H(X, Y)H(X,Y)	H(X,Y)=−∑x,yp(x,y)log⁡p(x,y)H(X, Y)=-\sum_{x,y}p(x,y)\log p(x,y)H(X,Y)=−∑x,yp(x,y)logp(x,y)	联合熵H(X,Y)H(X, Y)H(X,Y)表示XXX和YYY一起发生的不确定度
条件熵H(Y∣X)H(Y\|X)H(Y∣X)	H(Y∣X)=−∑x,yp(x,y)log⁡p(y∣x)H(Y\|X)=-\sum_{x,y}p(x,y)\log p(y\|x)H(Y∣X)=−∑x,yp(x,y)logp(y∣x)	条件熵H(Y∣X)H(Y\|X)H(Y∣X)表示XXX发生后，YYY的不确定度
条件熵H(X∣Y)H(X\|Y)H(X∣Y)	H(X∣Y)=−∑x,yp(x,y)log⁡p(x∣y)H(X\|Y)=-\sum_{x,y}p(x,y)\log p(x\|y)H(X∣Y)=−∑x,yp(x,y)logp(x∣y)	条件熵H(X∣Y)H(X\|Y)H(X∣Y)表示YYY发生后，XXX的不确定度
互信息I(X;Y)I(X;Y)I(X;Y)	I(X;Y)=H(X)−H(X∣Y)I(X;Y) = H(X)-H(X\|Y)I(X;Y)=H(X)−H(X∣Y); I(Y;X)=H(Y)−H(Y∣X)I(Y;X) = H(Y)-H(Y\|X)I(Y;X)=H(Y)−H(Y∣X); I(X;Y)=I(Y;X)I(X;Y) = I(Y;X)I(X;Y)=I(Y;X)	互信息I(X;Y)I(X;Y)I(X;Y)表示YYY发生后，XXX的不确定度减少了I(X;Y)I(X;Y)I(X;Y)

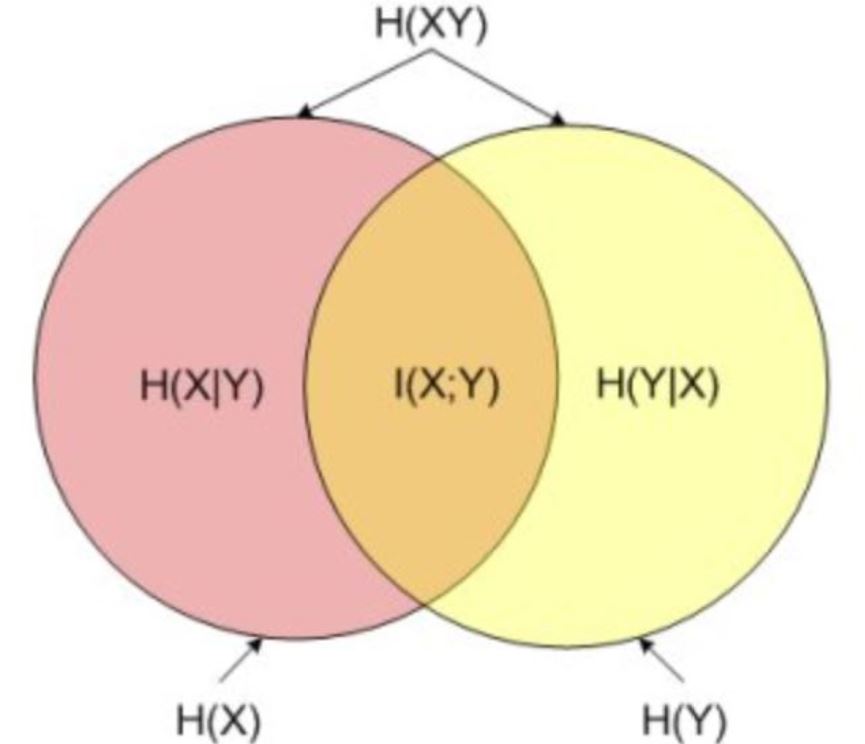
关系图：

曹雪虹, 张宗橙. 信息论与编码[J]. 2009. ↩︎
Shannon C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(4):379-423. ↩︎