模型的改善与泛化（梯度与等高线）

跟我一起机器学习系列文章将首发于公众号：月来客栈，欢迎文末扫码关注！

在上一篇文章中，笔者介绍了什么是等高线，并且还同时直接给出了梯度的垂直于等高线的结论，但是并没有介绍为什么。因此本篇文章就来大致介绍一下梯度为什么会垂直于等高线。

设f(x,y)=cf(x,y)=cf(x,y)=c为平面上任意一曲线，又由于曲线F(x,y)=0F(x,y)=0F(x,y)=0的法向量为n→={Fx,Fy}=ΔF\overrightarrow{n}=\{F_x,F_y\}=\Delta Fn={Fx,Fy}=ΔF。故，令F(x,y)=f(x,y)−c=0F(x,y)=f(x,y)-c=0F(x,y)=f(x,y)−c=0，立即有曲线F(x,y)F(x,y)F(x,y)的法向量为m→={fx,fy}\overrightarrow{m}=\{f_x,f_y\}m={fx,fy}。可以发现，曲线F(x,y)F(x,y)F(x,y)也就是f(x,y)=cf(x,y)=cf(x,y)=c的法向量m→\overrightarrow{m}m正好就是曲线f(x,y)=cf(x,y)=cf(x,y)=c对应的梯度，所以可以得出**梯度垂直于曲线（等高线）**的结论。

下面通过一个举例来说明：

如图所示，已知曲线f(x,y)=(x−2)2+y2−1=0f(x,y)=(x-2)^2+y^2-1=0f(x,y)=(x−2)2+y2−1=0，因此其在PPP点的梯度m→={2(x−2),2y}∣P\overrightarrow{m}=\{2(x-2),2y\}|_{P}m={2(x−2),2y}∣P。又因为曲线y=1−(x−2)2y=\sqrt{1-(x-2)^2}y=1−(x−2)2在PPP的斜率为：
k=2−x1−(x−2)2(1)k=\frac{2-x}{\sqrt{1-(x-2)^2}}\tag{1} k=1−(x−2)22−x(1)
将y=1−(x−2)2y=\sqrt{1-(x-2)^2}y=1−(x−2)2代入(1)(1)(1)得：
k=2−xy(2)k=\frac{2-x}{y}\tag{2} k=y2−x(2)
故，曲线y=1−(x−2)2y=\sqrt{1-(x-2)^2}y=1−(x−2)2过点PPP的切线的一个方向向量为n→={(y,2−x)}∣P\overrightarrow{n}=\{(y,2-x)\}|_Pn={(y,2−x)}∣P

注：若直线斜率为kkk，则他的一个方向向量为(1,k)(1,k)(1,k)

由此可得：m→⋅n→={2(x−2),2y}∣P⋅{(y,2−x)}∣P=0\overrightarrow{m}\cdot\overrightarrow{n}=\{2(x-2),2y\}|_{P}\cdot\{(y,2-x)\}|_P=0m⋅n={2(x−2),2y}∣P⋅{(y,2−x)}∣P=0

所以m→⊥n→\overrightarrow{m}\bot\overrightarrow{n}m⊥n，即曲线f(x,y)=(x−2)2+y2−1=0f(x,y)=(x-2)^2+y^2-1=0f(x,y)=(x−2)2+y2−1=0在任意一点的梯度m→\overrightarrow{m}m均垂直于曲线f(x,y)f(x,y)f(x,y)。

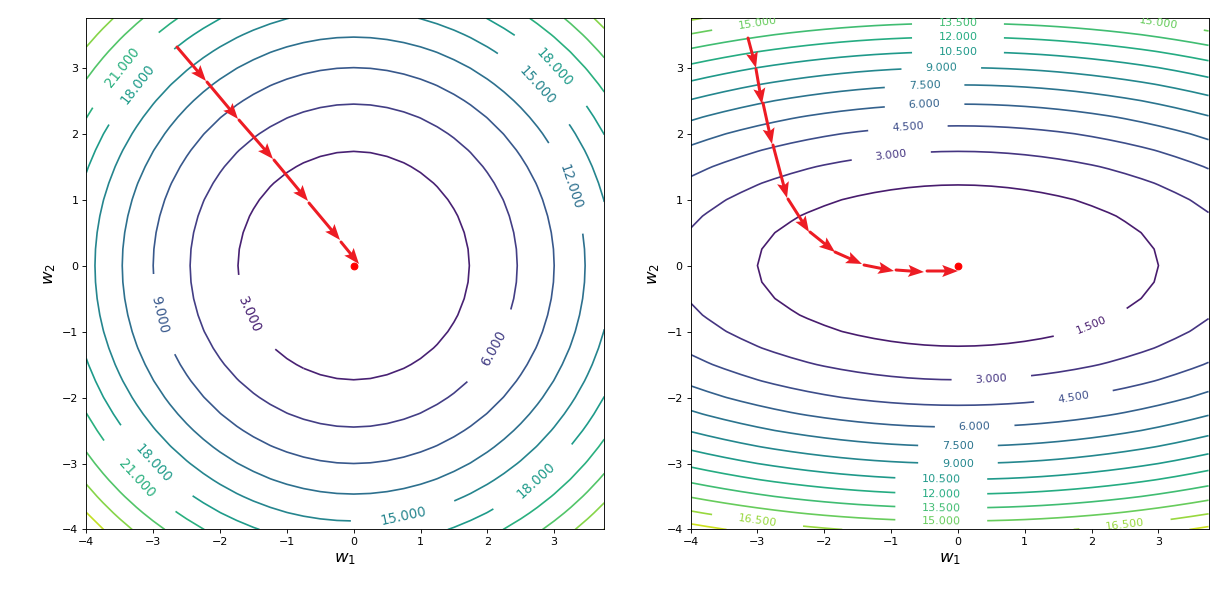
下图左边为随机选择一点，然后以梯度的反方向进行移动；右边为(0,0)(0,0)(0,0)点附近一点，然后以梯度方向进行移动：

引用

徐小湛《高等数学》第96讲方向导数与梯度
图示及示例代码：关注公众号回复“示例代码”即可直接获取！

模型的改善与泛化（梯度与等高线）相关推荐

深度学习WideDeep模型——记忆能力和泛化能力的综合
文章目录 Wide&Deep前言模型的记忆能力与泛化能力 Wide&Deep模型的结构 Wide&Deep前言 Wide&Deep模型的主要思路正如其名,是由单层的W ...
在深度学习模型的优化上，梯度下降并非唯一的选择
如果你是一名机器学习从业者,一定不会对基于梯度下降的优化方法感到陌生.对于很多人来说,有了 SGD,Adam,Admm 等算法的开源实现,似乎自己并不用再过多关注优化求解的细节.然而在模型的优化上,梯 ...
方向导数、梯度、等高线、数量场与向量场
转载自:http://blog.csdn.net/lijil168/article/details/69367531 之前用过几次梯度下降算法来求解一些优化问题,但对梯度的具体意义并不是很理解.前一段 ...
树模型为什么是不能进行梯度下降
对于树形结构为什么不需要归一化?机器学习 ML基础易答:数值缩放,不影响分裂点位置.因为第一步都是按照特征值进行排序的,排序的顺序不变,那么所属的分支以及分裂点就不会有不同.对于线性模型,比如说L ...
梯度下降（梯度，等高线）
文章目录梯度梯度例1 例2 结论梯度方向与等高线切线方向垂直 Q&A 梯度梯度梯度是矢量. 梯度方向就是函数值增加最快的方向. 例1 函数: z = x 2 + y 2 z=x^2 ...
隐私保护与生成模型: 差分隐私GAN的梯度脱敏方法
点击蓝字关注我们 AI TIME欢迎每一位AI爱好者的加入! 大规模数据的收集和利用大幅提升了机器学习算法的性能,但同时也令个人隐私保护面临更大的风险与挑战.为此,我们提出一种满足差分隐私(Diff ...
matlab仿真关键模型模块,改善simulink仿真的性能和精确度
一.加速仿真 1.模型包括一个MATLab Fcn模块.当执行一个包含MATLab Fcn模块的模型,Simulink在每一个仿真时间步都要调用MATLab 解释器.所以应尽可能地使用Simulink ...
svm多分类代码_跟我一起机器学习系列文章知识点与代码索引目录，持续更新…...
<跟我一起机器学习> 系列文章知识点与代码索引目录 0 环境配置如何才能入门机器学习? 优雅的安装和使用Anaconda 使用Conda来进行环境的创建与管理 Pycharm安装与使用 ...
Transformer性能被高估？DeepMind动态评估模型的时间泛化能力
©PaperWeekly 原创 · 作者 | 王馨月学校 | 四川大学研究方向 | 自然语言处理论文标题: Mind the Gap: Assessing Temporal Generaliza ...

模型的改善与泛化（梯度与等高线）

引用

模型的改善与泛化（梯度与等高线）相关推荐

最新文章

热门文章