在这一篇之前的内容是《Factor Analysis》，由于非常理论，打算学完整个课程后再写。在写这篇之前，我阅读了PCA、SVD和LDA。这几个模型相近，却都有自己的特点。本篇打算先介绍PCA，至于他们之间的关系，只能是边学边体会了。PCA以前也叫做Principal factor analysis。

1. 问题

真实的训练数据总是存在各种各样的问题：

1、 比如拿到一个汽车的样本，里面既有以“千米/每小时”度量的最大速度特征，也有“英里/小时”的最大速度特征，显然这两个特征有一个多余。

2、 拿到一个数学系的本科生期末考试成绩单，里面有三列，一列是对数学的兴趣程度，一列是复习时间，还有一列是考试成绩。我们知道要学好数学，需要有浓厚的兴趣，所以第二项与第一项强相关，第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢？

3、 拿到一个样本，特征非常多，而样例特别少，这样用回归去直接拟合非常困难，容易过度拟合。比如北京的房价：假设房子的特征是（大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数），搞了这么多特征，结果只有不到十个房子的样例。要拟合房子特征->房价的这么多特征，就会造成过度拟合。

4、 这个与第二个有点类似，假设在IR中我们建立的文档-词项矩阵中，有两个词项为“learn”和“study”，在传统的向量空间模型中，认为两者独立。然而从语义的角度来讲，两者是相似的，而且两者出现频率也类似，是不是可以合成为一个特征呢？

5、 在信号传输过程中，由于信道不是理想的，信道另一端收到的信号会有噪音扰动，那么怎么滤去这些噪音呢？

回顾我们之前介绍的《模型选择和规则化》，里面谈到的特征选择的问题。但在那篇中要剔除的特征主要是和类标签无关的特征。比如“学生的名字”就和他的“成绩”无关，使用的是互信息的方法。

而这里的特征很多是和类标签有关的，但里面存在噪声或者冗余。在这种情况下，需要一种特征降维的方法来减少特征数，减少噪音和冗余，减少过度拟合的可能性。

下面探讨一种称作主成分分析（PCA）的方法来解决部分上述问题。PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主元，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

2. PCA计算过程

首先介绍PCA的计算过程：

假设我们得到的2维数据如下：

行代表了样例，列代表特征，这里有10个样例，每个样例两个特征。可以这样认为，有10篇文档，x是10篇文档中“learn”出现的TF-IDF，y是10篇文档中“study”出现的TF-IDF。也可以认为有10辆汽车，x是千米/小时的速度，y是英里/小时的速度，等等。

第一步分别求x和y的平均值，然后对于所有的样例，都减去对应的均值。这里x的均值是1.81，y的均值是1.91，那么一个样例减去均值后即为（0.69,0.49），得到

第二步，求特征协方差矩阵，如果数据是3维，那么协方差矩阵是

这里只有x和y，求解得

对角线上分别是x和y的方差，非对角线上是协方差。协方差大于0表示x和y若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

第三步，求协方差的特征值和特征向量，得到

上面是两个特征值，下面是对应的特征向量，特征值0.0490833989对应特征向量为，这里的特征向量都归一化为单位向量。

第四步，将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

这里特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是。

第五步，将样本点投影到选取的特征向量上。假设样例数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(m*n)，协方差矩阵是n*n，选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为

这里是

FinalData(10*1) = DataAdjust(10*2矩阵)×特征向量

得到结果是

这样，就将原始样例的n维特征变成了k维，这k维就是原始特征在k维上的投影。

上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。

上述过程有个图描述：

正号表示预处理后的样本点，斜着的两条线就分别是正交的特征向量（由于协方差矩阵是对称的，因此其特征向量正交），最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。

如果取的k=2，那么结果是

这就是经过PCA处理后的样本数据，水平轴（上面举例为LS特征）基本上可以代表全部样本点。整个过程看起来就像将坐标系做了旋转，当然二维可以图形化表示，高维就不行了。上面的如果k=1，那么只会留下这里的水平轴，轴上是所有点在该轴的投影。

这样PCA的过程基本结束。在第一步减均值之后，其实应该还有一步对特征做方差归一化。比如一个特征是汽车速度（0到100），一个是汽车的座位数（2到6），显然第二个的方差比第一个小。因此，如果样本特征中存在这种情况，那么在第一步之后，求每个特征的标准差，然后对每个样例在该特征下的数据除以。

归纳一下，使用我们之前熟悉的表示方法，在求协方差之前的步骤是：

其中是样例，共m个，每个样例n个特征，也就是说是n维向量。是第i个样例的第j个特征。是样例均值。是第j个特征的标准差。

整个PCA过程貌似及其简单，就是求协方差的特征值和特征向量，然后做数据转换。但是有没有觉得很神奇，为什么求协方差的特征向量就是最理想的k维向量？其背后隐藏的意义是什么？整个PCA的意义是什么？

3. PCA理论基础

要解释为什么协方差矩阵的特征向量就是k维理想特征，我看到的有三个理论：分别是最大方差理论、最小错误理论和坐标轴相关度理论。这里简单探讨前两种，最后一种在讨论PCA意义时简单概述。

3.1 最大方差理论

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如前面的图，样本在横轴上的投影方差较大，在纵轴上的投影方差较小，那么认为纵轴上的投影是由噪声引起的。

因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。

比如下图有5个样本点：（已经做过预处理，均值为0，特征方差归一）

下面将样本投影到某一维上，这里用一条过原点的直线表示（前处理的过程实质是将原点移到样本点的中心点）。

假设我们选择两条不同的直线做投影，那么左右两条中哪个好呢？根据我们之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大。

这里先解释一下投影的概念：

红色点表示样例，蓝色点表示在u上的投影，u是直线的斜率也是直线的方向向量，而且是单位向量。蓝色点是在u上的投影点，离原点的距离是（即或者）由于这些样本点（样例）的每一维特征均值都为0，因此投影到u上的样本点（只有一个到原点的距离值）的均值仍然是0。

回到上面左右图中的左图，我们要求的是最佳的u，使得投影后的样本点方差最大。

由于投影后均值为0，因此方差为：

中间那部分很熟悉啊，不就是样本特征的协方差矩阵么（的均值为0，一般协方差矩阵都除以m-1，这里用m）。

用来表示，表示，那么上式写作

由于u是单位向量，即，上式两边都左乘u得，

即

We got it！就是的特征值，u是特征向量。最佳的投影直线是特征值最大时对应的特征向量，其次是第二大对应的特征向量，依次类推。

因此，我们只需要对协方差矩阵进行特征值分解，得到的前k大特征值对应的特征向量就是最佳的k维新特征，而且这k维新特征是正交的。得到前k个u以后，样例通过以下变换可以得到新的样本。

其中的第j维就是在上的投影。

通过选取最大的k个u，使得方差较小的特征（如噪声）被丢弃。

这是其中一种对PCA的解释，第二种是错误最小化，放在下一篇介绍。

3.2 最小平方误差理论

假设有这样的二维样本点（红色点），回顾我们前面探讨的是求一条直线，使得样本点投影到直线上的点的方差最大。本质是求直线，那么度量直线求的好不好，不仅仅只有方差最大化的方法。再回想我们最开始学习的线性回归等，目的也是求一个线性函数使得直线能够最佳拟合样本点，那么我们能不能认为最佳的直线就是回归后的直线呢？回归时我们的最小二乘法度量的是样本点到直线的坐标轴距离。比如这个问题中，特征是x，类标签是y。回归时最小二乘法度量的是距离d。如果使用回归方法来度量最佳直线，那么就是直接在原始样本上做回归了，跟特征选择就没什么关系了。

因此，我们打算选用另外一种评价直线好坏的方法，使用点到直线的距离d’来度量。

现在有n个样本点，每个样本点为m维（这节内容中使用的符号与上面的不太一致，需要重新理解符号的意义）。将样本点在直线上的投影记为，那么我们就是要最小化

这个公式称作最小平方误差（Least Squared Error）。

而确定一条直线，一般只需要确定一个点，并且确定方向即可。

第一步确定点：

假设要在空间中找一点来代表这n个样本点，“代表”这个词不是量化的，因此要量化的话，我们就是要找一个m维的点，使得

最小。其中是平方错误评价函数（squared-error criterion function），假设m为n个样本点的均值：

那么平方错误可以写作：

后项与无关，看做常量，而，因此最小化时，

是样本点均值。

第二步确定方向：

我们从拉出要求的直线（这条直线要过点m），假设直线的方向是单位向量e。那么直线上任意一点，比如就可以用点m和e来表示

其中是到点m的距离。

我们重新定义最小平方误差：

这里的k只是相当于i。就是最小平方误差函数，其中的未知参数是和e。

实际上是求的最小值。首先将上式展开：

我们首先固定e，将其看做是常量，，然后对进行求导，得

这个结果意思是说，如果知道了e，那么将与e做内积，就可以知道了在e上的投影离m的长度距离，不过这个结果不用求都知道。

然后是固定，对e求偏导数，我们先将公式（8）代入，得

其中 与协方差矩阵类似，只是缺少个分母n-1，我们称之为散列矩阵（scatter matrix）。

然后可以对e求偏导数，但是e需要首先满足，引入拉格朗日乘子，来使最大（最小），令

求偏导

这里存在对向量求导数的技巧，方法这里不多做介绍。可以去看一些关于矩阵微积分的资料，这里求导时可以将看作是，将看做是。

导数等于0时，得

两边除以n-1就变成了，对协方差矩阵求特征值向量了。

从不同的思路出发，最后得到同一个结果，对协方差矩阵求特征向量，求得后特征向量上就成为了新的坐标，如下图：

这时候点都聚集在新的坐标轴周围，因为我们使用的最小平方误差的意义就在此。

4. PCA理论意义

PCA将n个特征降维到k个，可以用来进行数据压缩，如果100维的向量最后可以用10维来表示，那么压缩率为90%。同样图像处理领域的KL变换使用PCA做图像压缩。但PCA要保证降维后，还要保证数据的特性损失最小。再看回顾一下PCA的效果。经过PCA处理后，二维数据投影到一维上可以有以下几种情况：

我们认为左图好，一方面是投影后方差最大，一方面是点到直线的距离平方和最小，而且直线过样本点的中心点。为什么右边的投影效果比较差？直觉是因为坐标轴之间相关，以至于去掉一个坐标轴，就会使得坐标点无法被单独一个坐标轴确定。

PCA得到的k个坐标轴实际上是k个特征向量，由于协方差矩阵对称，因此k个特征向量正交。看下面的计算过程。

假设我们还是用来表示样例，m个样例，n个特征。特征向量为e，表示第i个特征向量的第1维。那么原始样本特征方程可以用下面式子来表示：

前面两个矩阵乘积就是协方差矩阵（除以m后），原始的样本矩阵A是第二个矩阵m*n。

上式可以简写为

我们最后得到的投影结果是，E是k个特征向量组成的矩阵，展开如下：

得到的新的样例矩阵就是m个样例到k个特征向量的投影，也是这k个特征向量的线性组合。e之间是正交的。从矩阵乘法中可以看出，PCA所做的变换是将原始样本点（n维），投影到k个正交的坐标系中去，丢弃其他维度的信息。举个例子，假设宇宙是n维的（霍金说是11维的），我们得到银河系中每个星星的坐标（相对于银河系中心的n维向量），然而我们想用二维坐标去逼近这些样本点，假设算出来的协方差矩阵的特征向量分别是图中的水平和竖直方向，那么我们建议以银河系中心为原点的x和y坐标轴，所有的星星都投影到x和y上，得到下面的图片。然而我们丢弃了每个星星离我们的远近距离等信息。

5. 总结与讨论

这一部分来自http://www.cad.zju.edu.cn/home/chenlu/pca.htm

PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。

PCA技术的一个很大的优点是，它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。 
但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。

图表 4：黑色点表示采样数据，排列成转盘的形状。 
     容易想象，该数据的主元是_{或是旋转角。}

如图表 4中的例子，PCA找出的主元将是。但是这显然不是最优和最简化的主元。之间存在着非线性的关系。根据先验的知识可知旋转角是最优的主元（类比极坐标）。则在这种情况下，PCA就会失效。但是，如果加入先验的知识，对数据进行某种划归，就可以将数据转化为以为线性的空间中。这类根据先验知识对数据预先进行非线性转换的方法就成为kernel-PCA，它扩展了PCA能够处理的问题的范围，又可以结合一些先验约束，是比较流行的方法。

有时数据的分布并不是满足高斯分布。如图表 5所示，在非高斯分布的情况下，PCA方法得出的主元可能并不是最优的。在寻找主元时不能将方差作为衡量重要性的标准。要根据数据的分布情况选择合适的描述完全分布的变量，然后根据概率分布式

来计算两个向量上数据分布的相关性。等价的，保持主元间的正交假设，寻找的主元同样要使。这一类方法被称为独立主元分解(ICA)。

图表 5：数据的分布并不满足高斯分布，呈明显的十字星状。 
     这种情况下，方差最大的方向并不是最优主元方向。

另外PCA还可以用于预测矩阵中缺失的元素。

6. 其他参考文献

A tutorial on Principal Components Analysis LI Smith – 2002

A Tutorial on Principal Component Analysis J Shlens

http://www.cmlab.csie.ntu.edu.tw/~cyy/learning/tutorials/PCAMissingData.pdf

http://www.cad.zju.edu.cn/home/chenlu/pca.htm

PCA 简介

多元统计分析中普遍存在的困难中，有一个困难是多元数据的可视化。matlab 中的 plot 可以显示两个变量之间的关系，plot3 和surf 可以显示三维的不同。但是当有多于3个变量时，要可视化变量之间的关系就很困难了。

幸运的是，在一组多变量的数据中，很多变量常常是一起变动的。一个原因是很多变量是同一个驱动影响的的结果。在很多系统中，只有少数几个这样的驱动，但是多余的仪器使我们测量了很多的系统变量。当这种情况发生的时候，你需要处理的就是冗余的信息。而你可以通过用一个简单的新变量代替这组变量来简化此问题。

PCA 是一种较为常用的降维技术，PCA 的思想是将维特征映射到维上，这维是全新的正交特征。这维特征称为主元，是重新构造出来的维特征。在 PCA 中，数据从原来的坐标系转换到新的坐标系下，新的坐标系的选择与数据本身是密切相关的。其中，第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴选取的是与第一个坐标轴正交且具有最大方差的方向，依次类推，我们可以取到这样的个坐标轴。

PCA 操作流程

1. 去平均值，即每一位特征减去各自的平均值（当然，为避免量纲以及数据数量级差异带来的影响，先标准化是必要的）
2. 计算协方差矩阵
3. 计算协方差矩阵的特征值与特征向量
4. 对特征值从大到小排序
5. 保留最大的个特征向量
6. 将数据转换到个特征向量构建的新空间中

PCA 实例

考虑到实例的简洁性，这里只用二位数据。

假设二维数据为 data: 

取均值： 

• 去均值矩阵：

• 计算其协方差矩阵：

• 计算协方差矩阵的特征值和特征向量：

特征值为： 

特征向量为： 

• 对特征值进行排序（只有两个特征）

• 选择最大的特征值对应的特征向量： 
  

• 转换到新的空间 
  

由此，便实现了 PCA 降维操作。

MATLAB 实现 PCA

上面已经对 PCA 的算法过程做了详细说明，这里只针对 MATLAB 中的 PCA 函数作介绍并加以实例说明(详情也可参考 MATLAB 的PCA 文档，官方文档更加细致)：

[coef,score,latent] = pca(x);

• 1

x：为要输入的 n 维原始数据。带入这个 matlab 自带函数，将会生成新的 n 维加工后的数据（即 score）。此数据与之前的 n 维原始数据一一对应。

score：生成的n维加工后的数据存在 score 里。它是对原始数据进行的分析，进而在新的坐标系下获得的数据。他将这 n 维数据按贡献率由大到小排列。（即在改变坐标系的情况下，又对 n 维数据排序）。

latent：是一维列向量，每一个数据是对应 score 里相应维的贡献率，因为数据有 n 维所以列向量有n个数据。由大到小排列（因为 score 也是按贡献率由大到小排列）。

coef：是系数矩阵。通过 cofe 可以知道x是怎样转换成 score 的。

则模型为从原始数据出发： 
score = bsxfun(@minus,x,mean(x,1))*coef; (作用：可以把测试数据通过此方法转变为新的坐标系) 
逆变换： 
x = bsxfun(@plus,score*inv(coef),mean(x,1))

代码示例（此处选择一个10维度的数据集）：

%调用 pca 函数
[coef,score,latent,t2] = pca();score
%测试score是否和score_test一样
score_test=bsxfun(@minus,x,mean(x,1))*coef;
score_testlatent=100*latent/sum(latent)%将latent总和统一为100，便于观察贡献率
pareto(latent);%调用 matlab 画排列图

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

上图当贡献率累加至95%，以后的维数会不在显示，最多只显示10维。

几个注意点：

• PCA 针对的是 feature extraction ，而不是 feature 
  selection。PCA后会有贡献值，是输入者根据自己想要的贡献值进行维数的改变，进而生成数据。（一般大家会取贡献值在85%以上，要求高一点95%）。即在特征信息损失不多的情况下达到降维的目的。

• 主成分分析中 latent 显示的贡献值是加工后的数据的，并非原始数据。

• PCA分析，只根据输入数据的特征进行主成分分析，与输出有多少类型，每个数据对应哪个类型无关。考虑与聚类的结合，PCA 
  与聚类结果没有直接的关系。原因：PCA只是降低维度，簇并不一定与维度绑定，PCA 的作用顶多就是去掉噪音，减少计算量，并不会剔除簇信息。

学习图像处理，无疑会涉及到降维的操作，而PCA是常用的降维算法，既然经常用到，所以需要抠明白才行啊~~

PCA（PrincipalComponents Analysis）即主成分分析，是图像处理中经常用到的降维方法，大家知道，我们在处理有关数字图像处理方面的问题时，比如经常用的图像的查询问题，在一个几万或者几百万甚至更大的数据库中查询一幅相近的图像。

这时，我们通常的方法是对图像库中的图片提取响应的特征，如颜色，纹理，sift，surf，vlad等特征，然后将其保存，建立响应的数据索引，然后对要查询的图像提取相应的特征，与数据库中的图像特征对比，找出与之最近的图片。

这里，如果我们为了提高查询的准确率，通常会提取一些较为复杂的特征，如sift，surf等，一幅图像有很多个这种特征点，每个特征点又有一个相应的描述该特征点的128维的向量，设想如果一幅图像有300个这种特征点，那么该幅图像就有300*vector（128维）个，如果我们数据库中有一百万张图片，这个存储量是相当大的，建立索引也很耗时，如果我们对每个向量进行PCA处理，将其降维为64维，是不是很节约存储空间啊？

一、简介

PCA（Principal Components Analysis）即主成分分析，是图像处理中经常用到的降维方法，大家知道，我们在处理有关数字图像处理方面的问题时，比如经常用的图像的查询问题，在一个几万或者几百万甚至更大的数据库中查询一幅相近的图像。这时，我们通常的方法是对图像库中的图片提取响应的特征，如颜色，纹理，sift，surf，vlad等等特征，然后将其保存，建立响应的数据索引，然后对要查询的图像提取相应的特征，与数据库中的图像特征对比，找出与之最近的图片。这里，如果我们为了提高查询的准确率，通常会提取一些较为复杂的特征，如sift，surf等，一幅图像有很多个这种特征点，每个特征点又有一个相应的描述该特征点的128维的向量，设想如果一幅图像有300个这种特征点，那么该幅图像就有300*vector（128维）个，如果我们数据库中有一百万张图片，这个存储量是相当大的，建立索引也很耗时，如果我们对每个向量进行PCA处理，将其降维为64维，是不是很节约存储空间啊？对于学习图像处理的人来说，都知道PCA是降维的，但是，很多人不知道具体的原理，为此，我写这篇文章，来详细阐述一下PCA及其具体计算过程：

二、PCA详解

1、原始数据：

为了方便，我们假定数据是二维的，借助网络上的一组数据，如下：

x=[2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]T
y=[2.4, 0.7, 2.9, 2.2, 3.0, 2.7, 1.6, 1.1, 1.6, 0.9]T

2、计算协方差矩阵

什么是协方差矩阵？相信看这篇文章的人都学过数理统计，一些基本的常识都知道，但是，也许你很长时间不看了，都忘差不多了，为了方便大家更好的理解，这里先简单的回顾一下数理统计的相关知识，当然如果你知道协方差矩阵的求法你可以跳过这里。

（1）协方差矩阵：

首先我们给你一个含有n个样本的集合，依次给出数理统计中的一些相关概念：

均值：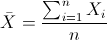
标准差：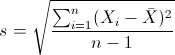
方差：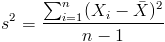

既然我们都有这么多描述数据之间关系的统计量，为什么我们还要用协方差呢？我们应该注意到，标准差和方差一般是用来描述一维数据的，但现实生活我们常常遇到含有多维数据的数据集，最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解这几科成绩之间的关系，这时，我们就要用协方差，协方差就是一种用来度量两个随机变量关系的统计量，其定义为：

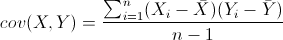
从协方差的定义上我们也可以看出一些显而易见的性质，如：

(X的方差)

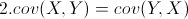
需要注意的是，协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

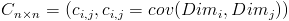
这个定义还是很容易理解的，我们可以举一个简单的三维的例子，假设数据集有三个维度，则协方差矩阵为

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。

（2）协方差矩阵的求法：

协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。下面我们将在matlab中用一个例子进行详细说明：

首先，随机产生一个10*3维的整数矩阵作为样本集，10为样本的个数，3为样本的维数。
MySample = fix(rand(10,3)*50)

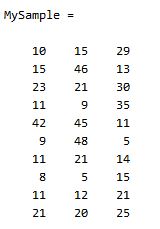
根据公式，计算协方差需要计算均值，那是按行计算均值还是按列呢，我一开始就老是困扰这个问题。前面我们也特别强调了，协方差矩阵是计算不同维度间的协方差，要时刻牢记这一点。样本矩阵的每行是一个样本，每列为一个维度，所以我们要按列计算均值。为了描述方便，我们先将三个维度的数据分别赋值：

dim1 = MySample(:,1);
dim2 = MySample(:,2);
dim3 = MySample(:,3);

计算dim1与dim2，dim1与dim3，dim2与dim3的协方差：

sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( size(MySample,1)-1 ) % 得到  74.5333
sum( (dim1-mean(dim1)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到  -10.0889
sum( (dim2-mean(dim2)) .* (dim3-mean(dim3)) ) / ( size(MySample,1)-1 ) % 得到  -10***000

搞清楚了这个后面就容易多了，协方差矩阵的对角线就是各个维度上的方差，下面我们依次计算：

std(dim1)^2 % 得到   108.3222
std(dim2)^2 % 得到   260.6222
std(dim3)^2 % 得到  94.1778

这样，我们就得到了计算协方差矩阵所需要的所有数据，调用Matlab自带的cov函数进行验证：

cov(MySample)

可以看到跟我们计算的结果是一样的，说明我们的计算是正确的。但是通常我们不用这种方法，而是用下面简化的方法进行计算：

先让样本矩阵中心化，即每一维度减去该维度的均值，然后直接用新的到的样本矩阵乘上它的转置，然后除以(N-1)即可。其实这种方法也是由前面的公式通道而来，只不过理解起来不是很直观而已。大家可以自己写个小的矩阵看一下就明白了。其Matlab代码实现如下：

X = MySample – repmat(mean(MySample),10,1);    % 中心化样本矩阵
C = (X’*X)./(size(X,1)-1)

（为方便对matlab不太明白的人，小小说明一下各个函数，同样，对matlab有一定基础的人直接跳过：

B = repmat(A,m,n ) %%将矩阵 A 复制 m×n 块，即把 A 作为 B 的元素，B 由 m×n 个 A 平铺而成。B 的维数是 [size(A,1)*m, (size(A,2)*n]

B = mean(A)的说明：

如果你有这样一个矩阵：A = [1 2 3; 3 3 6; 4 6 8; 4 7 7];
用mean(A)（默认dim=1）就会求每一列的均值
ans =
    3.0000    4.5000    6.0000
用mean(A,2)就会求每一行的均值 
ans =
    2.0000
    4.0000
    6.0000

6.0000

size(A,n)%% 如果在size函数的输入参数中再添加一项n，并用1或2为n赋值，则 size将返回矩阵的行数或列数。其中r=size(A,1)该语句返回的是矩阵A的行数， c=size(A,2) 该语句返回的是矩阵A的列数）

上面我们简单说了一下协方差矩阵及其求法，言归正传，我们用上面简化求法，求出样本的协方差矩阵为：

3、计算协方差矩阵的特征向量和特征值

因为协方差矩阵为方阵，我们可以计算它的特征向量和特征值，如下：

[eigenvectors,eigenvalues] = eig(cov)

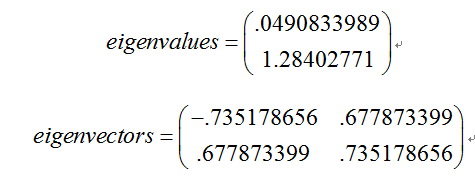
我们可以看到这些矢量都是单位矢量，也就是它们的长度为1，这对PCA来说是很重要的。

4、选择成分组成模式矢量

求出协方差矩阵的特征值及特征向量之后，按照特征值由大到小进行排列，这将给出成分的重要性级别。现在，如果你喜欢，可以忽略那些重要性很小的成分，当然这会丢失一些信息，但是如果对应的特征值很小，你不会丢失很多信息。如果你已经忽略了一些成分，那么最后的数据集将有更少的维数，精确地说，如果你的原始数据是n维的，你选择了前p个主要成分，那么你现在的数据将仅有p维。现在我们要做的是组成一个模式矢量，这只是几个矢量组成的矩阵的一个有意思的名字而已，它由你保持的所有特征矢量构成，每一个特征矢量是这个矩阵的一列。

对于我们的数据集，因为有两个特征矢量，因此我们有两个选择。我们可以用两个特征矢量组成模式矢量：

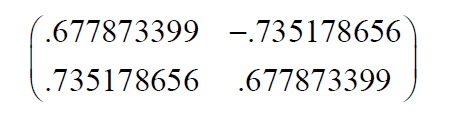
我们也可以忽略其中较小特征值的一个特征矢量，从而得到如下模式矢量：

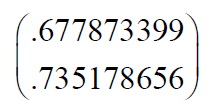
5、得到降维后的数据

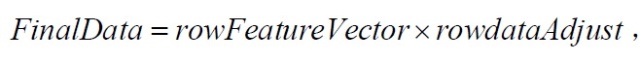
其中rowFeatureVector是由模式矢量作为列组成的矩阵的转置，因此它的行就是原来的模式矢量，而且对应最大特征值的特征矢量在该矩阵的最上一行。rowdataAdjust是每一维数据减去均值后，所组成矩阵的转置，即数据项目在每一列中，每一行是一维，对我们的样本来说即是，第一行为x维上数据，第二行为y维上的数据。FinalData是最后得到的数据，数据项目在它的列中，维数沿着行。

这将给我们什么结果呢？这将仅仅给出我们选择的数据。我们的原始数据有两个轴（x和y），所以我们的原始数据按这两个轴分布。我们可以按任何两个我们喜欢的轴表示我们的数据。如果这些轴是正交的，这种表达将是最有效的，这就是特征矢量总是正交的重要性。我们已经将我们的数据从原来的xy轴表达变换为现在的单个特征矢量表达。

（说明：如果要恢复原始数据，只需逆过程计算即可，即：

）

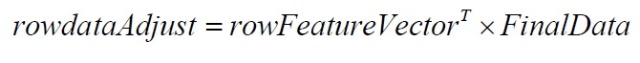
到此为止，相信你已经掌握了PCA及其原理了

转载请声明出处：http://blog.csdn.net/zhongkelee/article/details/44064401

一、PCA简介

1. 相关背景

上完陈恩红老师的《机器学习与知识发现》和季海波老师的《矩阵代数》两门课之后，颇有体会。最近在做主成分分析和奇异值分解方面的项目，所以记录一下心得体会。

在许多领域的研究与应用中，往往需要对反映事物的多个变量进行大量的观测，收集大量数据以便进行分析寻找规律。多变量大样本无疑会为研究和应用提供了丰富的信息，但也在一定程度上增加了数据采集的工作量，更重要的是在多数情况下，许多变量之间可能存在相关性，从而增加了问题分析的复杂性，同时对分析带来不便。如果分别对每个指标进行分析，分析往往是孤立的，而不是综合的。盲目减少指标会损失很多信息，容易产生错误的结论。

因此需要找到一个合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。由于各变量间存在一定的相关关系，因此有可能用较少的综合指标分别综合存在于各变量中的各类信息。主成分分析与因子分析就属于这类降维的方法。

2. 问题描述

下表1是某些学生的语文、数学、物理、化学成绩统计：

首先，假设这些科目成绩不相关，也就是说某一科目考多少分与其他科目没有关系。那么一眼就能看出来，数学、物理、化学这三门课的成绩构成了这组数据的主成分（很显然，数学作为第一主成分，因为数学成绩拉的最开）。为什么一眼能看出来？因为坐标轴选对了！下面再看一组学生的数学、物理、化学、语文、历史、英语成绩统计，见表2，还能不能一眼看出来：

数据太多了，以至于看起来有些凌乱！也就是说，无法直接看出这组数据的主成分，因为在坐标系下这组数据分布的很散乱。究其原因，是因为无法拨开遮住肉眼的迷雾~如果把这些数据在相应的空间中表示出来，也许你就能换一个观察角度找出主成分。如下图1所示：

但是，对于更高维的数据，能想象其分布吗？就算能描述分布，如何精确地找到这些主成分的轴？如何衡量你提取的主成分到底占了整个数据的多少信息？所以，我们就要用到主成分分析的处理方法。

3. 数据降维

为了说明什么是数据的主成分，先从数据降维说起。数据降维是怎么回事儿？假设三维空间中有一系列点，这些点分布在一个过原点的斜面上，如果你用自然坐标系x,y,z这三个轴来表示这组数据的话，需要使用三个维度，而事实上，这些点的分布仅仅是在一个二维的平面上，那么，问题出在哪里？如果你再仔细想想，能不能把x,y,z坐标系旋转一下，使数据所在平面与x,y平面重合？这就对了！如果把旋转后的坐标系记为x',y',z'，那么这组数据的表示只用x'和y'两个维度表示即可！当然了，如果想恢复原来的表示方式，那就得把这两个坐标之间的变换矩阵存下来。这样就能把数据维度降下来了！但是，我们要看到这个过程的本质，如果把这些数据按行或者按列排成一个矩阵，那么这个矩阵的秩就是2！这些数据之间是有相关性的，这些数据构成的过原点的向量的最大线性无关组包含2个向量，这就是为什么一开始就假设平面过原点的原因！那么如果平面不过原点呢？这就是数据中心化的缘故！将坐标原点平移到数据中心，这样原本不相关的数据在这个新坐标系中就有相关性了！有趣的是，三点一定共面，也就是说三维空间中任意三点中心化后都是线性相关的，一般来讲n维空间中的n个点一定能在一个n-1维子空间中分析！

上一段文字中，认为把数据降维后并没有丢弃任何东西，因为这些数据在平面以外的第三个维度的分量都为0。现在，假设这些数据在z'轴有一个很小的抖动，那么我们仍然用上述的二维表示这些数据，理由是我们可以认为这两个轴的信息是数据的主成分，而这些信息对于我们的分析已经足够了，z'轴上的抖动很有可能是噪声，也就是说本来这组数据是有相关性的，噪声的引入，导致了数据不完全相关，但是，这些数据在z'轴上的分布与原点构成的夹角非常小，也就是说在z'轴上有很大的相关性，综合这些考虑，就可以认为数据在x',y' 轴上的投影构成了数据的主成分！

课堂上老师谈到的特征选择的问题，其实就是要剔除的特征主要是和类标签无关的特征。而这里的特征很多是和类标签有关的，但里面存在噪声或者冗余。在这种情况下，需要一种特征降维的方法来减少特征数，减少噪音和冗余，减少过度拟合的可能性。

PCA的思想是将n维特征映射到k维上（k<n），这k维是全新的正交特征。这k维特征称为主成分，是重新构造出来的k维特征，而不是简单地从n维特征中去除其余n-k维特征。

二、PCA实例

现在假设有一组数据如下：

行代表了样例，列代表特征，这里有10个样例，每个样例两个特征。可以这样认为，有10篇文档，x是10篇文档中“learn”出现的TF-IDF，y是10篇文档中“study”出现的TF-IDF。

第一步，分别求x和y的平均值，然后对于所有的样例，都减去对应的均值。这里x的均值是1.81，y的均值是1.91，那么一个样例减去均值后即为（0.69,0.49），得到

第二步，求特征协方差矩阵，如果数据是3维，那么协方差矩阵是

这里只有x和y，求解得

对角线上分别是x和y的方差，非对角线上是协方差。协方差是衡量两个变量同时变化的变化程度。协方差大于0表示x和y若一个增，另一个也增；小于0表示一个增，一个减。如果ｘ和ｙ是统计独立的，那么二者之间的协方差就是０；但是协方差是０，并不能说明ｘ和ｙ是独立的。协方差绝对值越大，两者对彼此的影响越大，反之越小。协方差是没有单位的量，因此，如果同样的两个变量所采用的量纲发生变化，它们的协方差也会产生树枝上的变化。

第三步，求协方差的特征值和特征向量，得到

上面是两个特征值，下面是对应的特征向量，特征值0.0490833989对应特征向量为，这里的特征向量都归一化为单位向量。

第四步，将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

这里特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是(-0.677873399, -0.735178656)T。

第五步，将样本点投影到选取的特征向量上。假设样例数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(m*n)，协方差矩阵是n*n，选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为

FinalData(10*1) = DataAdjust(10*2矩阵) x 特征向量(-0.677873399, -0.735178656)T

得到的结果是

这样，就将原始样例的n维特征变成了k维，这k维就是原始特征在k维上的投影。

上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。上述过程如下图2描述：

正号表示预处理后的样本点，斜着的两条线就分别是正交的特征向量（由于协方差矩阵是对称的，因此其特征向量正交），最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。

整个PCA过程貌似及其简单，就是求协方差的特征值和特征向量，然后做数据转换。但是有没有觉得很神奇，为什么求协方差的特征向量就是最理想的k维向量？其背后隐藏的意义是什么？整个PCA的意义是什么？

三、PCA推导

先看下面这幅图：

在第一部分中，我们举了一个学生成绩的例子，里面的数据点是六维的，即每个观测值是6维空间中的一个点。我们希望将6维空间用低维空间表示。

先假定只有二维，即只有两个变量，它们由横坐标和纵坐标所代表；因此每个观测值都有相应于这两个坐标轴的两个坐标值；如果这些数据形成一个椭圆形状的点阵，那么这个椭圆有一个长轴和一个短轴。在短轴方向上，数据变化很少；在极端的情况，短轴如果退化成一点，那只有在长轴的方向才能够解释这些点的变化了；这样，由二维到一维的降维就自然完成了。

上图中，u1就是主成分方向，然后在二维空间中取和u1方向正交的方向，就是u2的方向。则n个数据在u1轴的离散程度最大（方差最大），数据在u1上的投影代表了原始数据的绝大部分信息，即使不考虑u2，信息损失也不多。而且，u1、u2不相关。只考虑u1时，二维降为一维。

椭圆的长短轴相差得越大，降维也越有道理。

1. 最大方差理论

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如前面的图，样本在u1上的投影方差较大，在u2上的投影方差较小，那么可认为u2上的投影是由噪声引起的。

因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。

比如我们将下图中的5个点投影到某一维上，这里用一条过原点的直线表示（数据已经中心化）：

假设我们选择两条不同的直线做投影，那么左右两条中哪个好呢？根据我们之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大（也可以说是投影的绝对值之和最大）。

计算投影的方法见下图5：

图中，红色点表示样例，蓝色点表示在u上的投影，u是直线的斜率也是直线的方向向量，而且是单位向量。蓝色点是在u上的投影点，离原点的距离是<x,u>（即xTu或者uTx）。

2. 最小二乘法

我们使用最小二乘法来确定各个主轴（主成分）的方向。

对给定的一组数据（下面的阐述中，向量一般均指列向量）：

其数据中心位于:

数据中心化（将坐标原点移到样本点的中心点）：

中心化后的数据在第一主轴u1方向上分布散的最开，也就是说在u1方向上的投影的绝对值之和最大（也可以说方差最大），计算投影的方法上面已经阐述，就是将x与u1做内积，由于只需要求u1的方向，所以设u1也是单位向量。

在这里，也就是最大化下式：

由矩阵代数相关知识可知，可以对绝对值符号项进行平方处理，比较方便。所以进而就是最大化下式：

两个向量做内积，可以转化成矩阵乘法：

所以目标函数可以表示为：

括号里面就是矩阵乘法表示向量内积，由于列向量转置以后是行向量，行向量乘以列向量得到一个数，一个数的转置还是其本身，所以又可以将目标函数化为：

去括号：

又由于u1和i无关，可以拿到求和符外面，上式化简为：

学过矩阵代数的同学可能已经发现了，上式括号里面求和后的结果，就相当于一个大矩阵乘以自身的转置，其中，这个大矩阵的形式如下：

X矩阵的第i列就是xi

于是有：

所以目标函数最终化为：

其中的就是一个二次型，

我们假设的某一特征值为λ，对应的特征向量为ξ，有

所以，是半正定的对称矩阵，即是半正定阵的二次型，由矩阵代数知识得出，目标函数存在最大值！

下面我们求解最大值、取得最大值时u1的方向这两个问题。

先解决第一个问题，对于向量x的二范数平方为:

同样，目标函数也可以表示成映射后的向量的二范数平方：

把二次型化成一个范数的形式，由于u1取单位向量，最大化目标函数的基本问题也就转化为：对一个矩阵，它对一个向量做变换，变换前后的向量的模长伸缩尺度如何才能最大？我们有矩阵代数中的定理知，向量经矩阵映射前后的向量长度之比的最大值就是这个矩阵的最大奇异值，即：

式中，是矩阵A的最大奇异值（亦是矩阵A的二范数），它等于（或）的最大特征值开平方。

针对本问题来说，是半正定对称阵，也就意味着它的特征值都大于等于0，且不同特征值对应的特征向量是正交的，构成所在空间的一组单位正交基。

再解决第二个问题，对一般情况，设对称阵的n个特征值分别为：

相应的单位特征向量为：

任取一个向量x，用特征向量构成的空间中的这组基表示为：

则：

所以：

针对第二个问题，我们取上式中的，目标函数取得最大值，也就是的最大特征值时，对应的特征向量的方向，就是第一主成分u1的方向！（第二主成分的方向为的第二大特征值对应的特征向量的方向，以此类推）。

证明完毕。

主成分所占整个信息的百分比可用下式计算：

式中分母为所有奇异值平方和，分子为所选取的前k大奇异值平方和。

有些研究工作表明，所选的主轴总长度占所有主轴长度之和的大约85% 即可，其实，这只是一个大体的说法，具体选多少个，要看实际情况而定。

3.意义

PCA将n个特征降维到k个，可以用来进行数据压缩，例如100维的向量最后可以用10维来表示，那么压缩率为90%。同样图像处理领域的KL变换使用PCA做图像压缩，人脸检测和匹配。比如如下摘自另一篇博客上的Matlab实验结果：

可见测试样本为人脸的样本的重建误差显然小于非人脸的重建误差。

另外PCA还可以联系奇异值分解（SVD），来用于预测矩阵中缺失的元素，可以应用到评分预测等实际项目中。详见后续SVD的博客。

有问题或者想法可以和我交流：lichunchun4.0@gmail.com

转载请声明出处：http://blog.csdn.net/zhongkelee/article/details/44064401