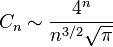Catalan卡塔兰数
卡塔兰数
卡塔兰数是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。
卡塔兰数的一般项公式为 
另类递归式: h(n)=((4*n-2)/(n+1))*h(n-1);
前几项为: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
性质
Cn的另一个表达形式为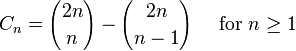
所以,Cn是一个自然数;这一点在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。(见下文的第二个证明。)
卡塔兰数满足以下递推关系
它也满足
这提供了一个更快速的方法来计算卡塔兰数。
卡塔兰数的渐近增长为
它的含义是左式除以右式的商趋向于1当n → ∞。(这可以用n!的斯特灵公式来证明。)
所有的奇卡塔兰数Cn都满足n = 2k − 1。所有其他的卡塔兰数都是偶数。
应用
组合数学中有非常多.的组合结构可以用卡塔兰数来计数。在Richard P. Stanley的Enumerative Combinatorics: Volume 2一书的习题中包括了66个相异的可由卡塔兰数表达的组合结构。以下用Cn=3和Cn=4举若干例:
- Cn表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串,且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
- 将上例的X换成左括号,Y换成右括号,Cn表示所有包含n组括号的合法运算式的个数:
((())) ()(()) ()()() (())() (()())
- Cn表示有n+1个叶子的二叉树的个数。

- Cn表示所有不同构的含n个分枝结点的满二叉树的个数。(一个有根二叉树是满的当且仅当每个结点都有两个子树或没有子树。)
证明:
令1表示进栈,0表示出栈,则可转化为求一个2n位、含n个1、n个0的二进制数,满足从左往右扫描到任意一位时,经过的0数不多于1数。显然含n个1、n个0的2n位二进制数共有 个,下面考虑不满足要求的数目.
个,下面考虑不满足要求的数目.
考虑一个含n个1、n个0的2n位二进制数,扫描到第2m+1位上时有m+1个0和m个1(容易证明一定存在这样的情况),则后面的0-1排列中必有n-m个1和n-m-1个0。将2m+2及其以后的部分0变成1、1变成0,则对应一个n+1个0和n-1个1的二进制数。反之亦然(相似的思路证明两者一一对应)。
从而 。证毕。
。证毕。
- Cn表示所有在n × n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发,在格点右上角结束,每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数: X代表“向右”,Y代表“向上”。下图为n = 4的情况:
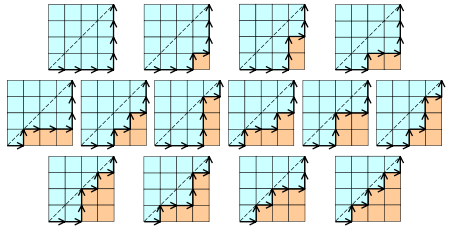
- Cn表示通过连结顶点而将n + 2边的凸多边形分成三角形的方法个数。下图中为n = 4的情况:
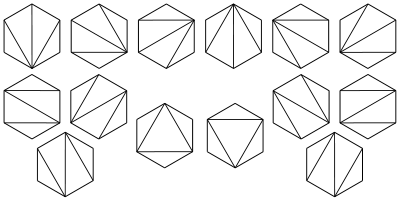
- Cn表示对{1, ..., n}依序进出栈的置换个数。一个置换w是依序进出栈的当S(w) = (1, ..., n), 其中S(w)递归定义如下:令w = unv,其中n为w的最大元素,u和v为更短的数列;再令S(w) =S(u)S(v)n,其中S为所有含一个元素的数列的单位元。
- Cn表示集合{1, ..., n}的不交叉划分的个数. 那么, Cn 永远不大于第n项贝尔数. Cn也表示集合{1, ..., 2n}的不交叉划分的个数,其中每个段落的长度为2。综合这两个结论,可以用数学归纳法证明 that all of the free cumulants of degree more than 2 of the Wigner semicircle law are zero. This law is important in free probability theory and the theory of random matrices.
- Cn表示用n个长方形填充一个高度为n的阶梯状图形的方法个数。下图为 n = 4的情况:

我总结了一下,最典型的四类应用:(实质上却都一样,无非是递归等式的应用,就看你能不能分解问题写出递归式了)
1.括号化问题。
矩阵链乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?(h(n)种)
2.出栈次序问题。
一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
类似:
(1)有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
(2)在圆上选择2n个点,将这些点成对连接起来,使得所得到的n条线段不相交的方法数。
3.将多边行划分为三角形问题。
将一个凸多边形区域分成三角形区域的方法数?
类似:一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她
从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
类似:在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
4.给顶节点组成二叉树的问题。
给定N个节点,能构成多少种形状不同的二叉树?
(一定是二叉树!
先去一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) +  + h(n-1)h(0)=h(n))
+ h(n-1)h(0)=h(n))
(能构成h(N)个)
转载于:https://www.cnblogs.com/yxh-amysear/p/8260440.html
Catalan卡塔兰数相关推荐
- C语言实现卡塔兰数catalan(附完整源码)
实现卡塔兰数catalan 实现卡塔兰数catalan完整源码(定义,实现,main函数测试) 实现卡塔兰数catalan完整源码(定义,实现,main函数测试) #include <stdio ...
- 卡塔兰数(Catalan Number)--动态规划(Dynamic Programming)
-卡塔兰数是组合数学中一个常在各种计数问题中出现的数列.以比利时的数学家欧仁·查理·卡特兰(1814–1894)命名.历史上,清朝数学家明安图(1692年-1763年)在其<割圜密率捷法> ...
- 【卡塔兰数】LeetCode 96. Unique Binary Search Trees
LeetCode 96. Unique Binary Search Trees 本博客转载自:http://www.cnblogs.com/grandyang/p/4299608.html Solut ...
- 卡特兰数 卡塔兰数 概念 代码实现 模型分析全集
特别鸣谢 参考1 参考2 参考3 概念 情境导入 一个栈(无穷大)的进栈序列为1,2,3,-,n,有多少个不同的出栈序列? 可以形象化地转化为括号问题,更好理解,进栈是(,出栈是),下面为n=3的全部 ...
- leetcode(96)不同的二叉搜索树——卡塔兰数
题目描述 给定一个整数 n,求以 1 - n 为节点组成的二叉搜索树有多少种? 示例: 输入: 3 输出: 5 解释: 给定 n = 3, 一共有 5 种不同结构的二叉搜索树:1 3 3 2 1\ / ...
- 卡塔兰数(Catlan)
refernce: http://zh.wikipedia.org/wiki/%E5%8D%A1%E5%A1%94%E5%85%B0%E6%95%B0 卡塔兰数是组合数学中一个常在各种计数问题中出现的 ...
- 卡塔兰数用于求解不同形态的二叉树的数目,题目选自CS61A2021 LAB9 Q3: Number of Trees
完全二叉树是一种每个节点都有2个分支或0个分支,但从来没有1个分支的树. 编写一个函数,返回恰好有n个叶结点的唯一完整二叉树结构的数目. 对于那些对组合学感兴趣的人来说,这个问题确实有一个封闭形式的解 ...
- 卡特兰数(卡塔兰数)
卡特兰数(卡塔兰数) 另附图一张: 来源:百度百科 典例: hdu 2067 小兔的棋盘 Problem Description 小兔的叔叔从外面旅游回来给她带来了一个礼物,小兔高兴地跑回自己的房间, ...
- 洛谷P1722 矩阵Ⅱ (卡塔兰数)
洛谷P1722 矩阵Ⅱ 卡塔兰数 题面 思路 代码 题面 给定一个1*(2n)的矩阵.现让你放入一样多的红色算筹和黑色算筹,使对于所有的i(1<=i<=2n),使第1~i格中红色算筹个数大 ...
最新文章
- jquery mobile app案例_讲座预告 | 运动app内的个人成就、运动轨迹和社交分享对体能提升的长期效应研究...
- LBWE 和SBIW的关系
- (一)Linux基础(1)
- 模糊逻辑系统_在模糊逻辑系统中工作 人工智能
- watch监控,对比新值和旧值做出相应判断
- 第一章 进程与线程的基本概念
- springboot在启动jar由于配置hibernate的映射文件上classpath导致的!BOOT-INF/classes/!路径出现!号问题解决方法
- bundle java_Bundle类
- python入门到熟练要多久_python_入门到熟练_day02
- banner设圆角_Banner设计技巧!
- Hbase中的二级索引
- 《Python 深度学习》刷书笔记 Chapter 8 Part-2 用Keras 实现 DeepDream
- 蓝天P7xxtm 系列9代最新BIOS
- Javascript removeChild()删除节点及删除子节点的方法
- 中班音乐活动计算机反思,中班音乐优质教案《计算器》含反思
- 【githubshare】深度学习蘑菇书,覆盖了强化学习、马尔可夫决策过程、策略梯度、模仿学习
- 100多个优秀的互联网编程学习平台整理。
- 剑指offter 数据结构之数组
- 服务器虚拟化技术简介,服务器虚拟化技术简介
- Hi35XXX海思媒体处理平台架构介绍.
热门文章
- mysql存储过程实例_mysql存储过程案例讲解
- 异星工厂 自动机器人_刚刚,ABB机器人全球最大机器人超级工厂在康桥动工! 投资10亿元,用机器人造机器人...
- java api 测试工具_Java 实现在线HTTP接口测试 - HTTP GET/POST模拟请求测试工具
- f分布表完整图_分布式计算引擎之星——Spark
- (2)stm32开发之使用Keil MDK以及标准外设库创建STM32工程
- 车辆姿态相关的传感器概述
- 电源纹波分析及测试方法
- Linux查看和剔除当前登录用户
- angularjs directive 实例 详解
- Windows7上安装TensorFlow——基于Docker镜像