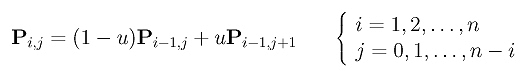最近有一个需求是这样的：点赞后变化的数字从VIew的底部上浮到label的text的对应的需要改变的数字位置，替换该数字。（也就是说，如果点赞前该数字是158，点赞后变成159，那么从View底部飘上来的数字只有9）。实现这个路径动画有多种方法，首次尝试使用CAKeyframeAnimation+贝塞尔曲线绘图。

下面是贝塞尔曲线的实现原理：

贝塞尔曲线，可以通过三个点，来确定一条平滑的曲线。在计算机图形学应该有讲。是图形开发中的重要工具。

实现的是一个图形做圆周运动。不过不是简单的关键帧动画那样，是计算出了很多点，当然还是用的关键帧动画，即使用CAKeyframeAnimation。有了贝塞尔曲线的支持，可以赋值给CAKeyframeAnimation 贝塞尔曲线的Path引用。

用贝塞尔曲线画圆，是一种特殊情况，我的做法是通过贝塞尔曲线得到4个半圆的曲线，它们合成的路径就是整个圆。

以下是动画部分的代码：

- (void) doAnimation { 
    CAKeyframeAnimation *animation=[CAKeyframeAnimation animationWithKeyPath:@"position"]; 
    animation.duration=10.5f; 
    animation.removedOnCompletion = NO; 
    animation.fillMode = kCAFillModeForwards; 
    animation.repeatCount=HUGE_VALF;// repeat forever 
    animation.calculationMode = kCAAnimationCubicPaced; 
    
    CGMutablePathRef curvedPath = CGPathCreateMutable(); 
    CGPathMoveToPoint(curvedPath, NULL, 512, 184);

　　//增加4个二阶贝塞尔曲线
    CGPathAddQuadCurveToPoint(curvedPath, NULL, 312, 184, 312, 384); 
    CGPathAddQuadCurveToPoint(curvedPath, NULL, 310, 584, 512, 584); 
    CGPathAddQuadCurveToPoint(curvedPath, NULL, 712, 584, 712, 384); 
    CGPathAddQuadCurveToPoint(curvedPath, NULL, 712, 184, 512, 184); 
    
    animation.path=curvedPath; 
    
    [flyStarLayer addAnimation:animation forKey:nil]; 
}

Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。 曲线定义：起始点、终止点（也称锚点）、控制点。通过调整控制点，贝塞尔曲线的形状会发生变化。 1962年，法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法，并给出了详细的计算公式，因此按照这样的公式绘制出来的曲线就用他的姓氏来命名，称为贝塞尔曲线。

以下公式中：B(t)为t时间下 点的坐标；

P0为起点,Pn为终点,Pi为控制点

一阶贝塞尔曲线(线段)：

意义：由 P0 至 P1 的连续点， 描述的一条线段

二阶贝塞尔曲线(抛物线)：

原理：由 P0 至 P1 的连续点 Q0，描述一条线段。 
      由 P1 至 P2 的连续点 Q1，描述一条线段。 
      由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线。

经验：P1-P0为曲线在P0处的切线。

三阶贝塞尔曲线：

通用公式：

高阶贝塞尔曲线：

4阶曲线：

5阶曲线：

http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/de-casteljau.html

Following the construction of a Bézier curve, the next important task is to find the point C(u) on the curve for a particular u. A simple way is to plug u into every basis function, compute the product of each basis function and its corresponding control point, and finally add them together. While this works fine, it is not numerically stable (i.e., could introduce numerical errors during the course of evaluating the Bernstein polynomials).

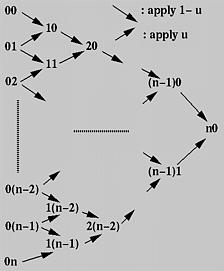
In what follows, we shall only write down the control point numbers. That is, the control points are 00 for P0, 01 for P1, ..., 0i for Pi, ..., 0n for Pn. The 0s in these numbers indicate the initial or the 0-th iteration. Later on, it will be replaced with 1, 2, 3 and so on.

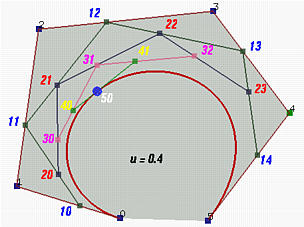
The fundamental concept of de Casteljau's algorithm is to choose a point C in line segment AB such that C divides the line segment AB in a ratio of u:1-u (i.e., the ratio of the distance between A and C and the distance between A and B is u). Let us find a way to determine the point C.

The vector from A to B is B - A. Since u is a ratio in the range of 0 and 1, point C is located at u(B - A). Taking the position of A into consideration, point C is A + u(B - A) = (1 - u)A + uB. Therefore, given a u, (1 - u)A + uB is the point C between A and B that divides AB in a ratio of u:1-u.

The idea of de Casteljau's algorithm goes as follows. Suppose we want to find C(u), where u is in [0,1]. Starting with the first polyline, 00-01-02-03...-0n, use the above formula to find a point 1i on the leg (i.e. line segment) from 0i to0(i+1) that divides the line segment 0i and 0(i+1) in a ratio of u:1-u. In this way, we will obtain n points 10, 11, 12, ...., 1(n-1). They define a new polyline of n - 1 legs.

In the figure above, u is 0.4. 10 is in the leg of 00 and 01, 11 is in the leg of 01 and 02, ..., and 14 is in the leg of04 and 05. All of these new points are in blue.

The new points are numbered as 1i's. Apply the procedure to this new polyline and we shall get a second polyline of n - 1 points 20, 21, ..., 2(n-2) and n - 2 legs. Starting with this polyline, we can construct a third one of n - 2 points 30,31, ..., 3(n-3) and n - 3 legs. Repeating this process n times yields a single point n0. De Casteljau proved that this is the point C(u) on the curve that corresponds to u.

Let us continue with the above figure. Let 20 be the point in the leg of 10 and 11 that divides the line segment 10 and 11in a ratio of u:1-u. Similarly, choose 21 on the leg of 11 and 12, 22 on the leg of 12 and 13, and 23 on the leg of 13and 14. This gives a third polyline defined by 20, 21, 22 and 23. This third polyline has 4 points and 3 legs. Keep doing this and we shall obtain a new polyline of three points 30, 31 and 32. From this fourth polyline, we have the fifth one of two points 40 and 41. Do it once more, and we have 50, the point C(0.4) on the curve.

This is the geometric interpretation of de Casteljau's algorithm, one of the most elegant result in curve design.

Actual Computation

Given the above geometric interpretation of de Casteljau's algorithm, we shall present a computation method, which is shown in the following figure.

First, all given control points are arranged into a column, which is the left-most one in the figure. For each pair of adjacent control points, draw a south-east bound arrow and a north-east bound arrow, and write down a new point at the intersection of the two adjacent arrows. For example, if the two adjacent points are ij and i(j+1), the new point is(i+1)j. The south-east (resp., north-east) bound arrow means multiplying 1 - u (resp., u) to the point at its tail, ij(resp., i(j+1)), and the new point is the sum.

Thus, from the initial column, column 0, we compute column 1; from column 1 we obtain column 2 and so on. Eventually, aftern applications we shall arrive at a single point n0 and this is the point on the curve. The following algorithm summarizes what we have discussed. It takes an array P of n+1 points and a u in the range of 0 and 1, and returns a point on the Bézier curve C(u).

  • Q

    • [

    i

    • ] :=

    P

    • [

    i

    • ]; // save input
    • Q

      • [

      i

      • ] := (1 -

      u

      • )

      Q

      • [

      i

      • ] +

      u

      Q

      • [

      i

      • + 1];

      for i := 0 to n - k do

    Input: array P[0:n] of n+1 points and real number u in [0,1] 
    Output: point on curve, C(u) 
    Working: point array Q[0:n]

    for i := 0 to n do 
    for     k := 1 to n do 
    return Q    [0];

A Recurrence Relation

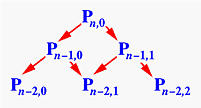
The above computation can be expressed recursively. Initially, let P0,j be Pj for j = 0, 1, ..., n. That is, P0,j is the j-th entry on column 0. The computation of entry j on column i is the following:

More precisely, entry Pi,j is the sum of (1-u)Pi-1,j (upper-left corner) and uPi-1,j+1 (lower-left corner). The final result (i.e., the point on the curve) is Pn,0. Based on this idea, one may immediately come up with the following recursive procedure:

    • return P0,j

      return

      • (1-

      u

      • )*

       deCasteljau

      • (

      i

      • -1,

      j

      • ) +

      u

      • *

       deCasteljau

      • (

      i

      • -1,

      j

      • +1)

      if i = 0 then 
      else

    function deCasteljau(i,j) 
    begin 
    end

This procedure looks simple and short; however, it is extremely inefficient. Here is why. We start with a call todeCasteljau(n,0) for computing Pn,0. The else part splits this call into two more calls, deCasteljau(n-1,0) for computing Pn-1,0 and deCasteljau(n-1,1) for computing Pn-1,1.

Consider the call to deCasteljau(n-1,0). It splits into two more calls, deCasteljau(n-2,0) for computing Pn-2,0 anddeCasteljau(n-2,1) for computing Pn-2,1. The call to deCasteljau(n-1,1) splits into two calls, deCasteljau(n-2,1) for computing Pn-2,1 and deCasteljau(n-2,2) for computing Pn-2,2. Thus, deCasteljau(n-2,1) is called twice. If we keep expanding these function calls, we should discover that almost all function calls for computing Pi,j are repeated, not once but many times. How bad is this? In fact, the above computation scheme is identical to the following way of computing then-th Fibonacci number:

    • return

      • 1

      return

      Fibonacci

      • (

      n

      • -1) +

      Fibonacci

      • (

      n

      • -2)

      if n = 0 or n = 1 then 
      else

    function Fibonacci(n)
    beginend

This program takes an exponential number of function calls (an exercise) to compute Fibonacci(n). Therefore, the above recursive version of de Casteljau's algorithm is not suitable for direct implementation, although it looks simple and elegant!

An Interesting Observation

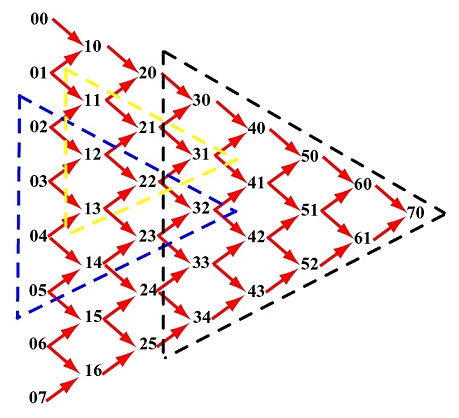
The triangular computation scheme of de Casteljau's algorithm offers an interesting observation. Take a look at the following computation on a Bézier curve of degree 7 defined by 8 control points 00, 01, ..., 07. Let us consider a set of consecutive points on the same column as the control points of a Bézier curve. Then, given a u in [0,1], how do we compute the corresponding point on this Bézier curve? If de Casteljau's algorithm is applied to these control points, the point on the curve is the opposite vertex of the equilateral's base formed by the selected points!

For example, if the selected points are 02, 03, 04 and 05, the point on the curve defined by these four control points that corresponds to u is 32. See the blue triangle. If the selected points are 11, 12 and 13, the point on the curve is31. See the yellow triangle. If the selected points are 30, 31, 32, 33 and 34, the point on the curve is 70.

By the same reason, 70 is the point on the Bézier curve defined by control points 60 and 61. It is also the point on the curve defined by 50, 51 and 52, and on the curve defined by 40, 41, 42 and 43. In general, if we select a point and draw an equilateral as shown above, the base of this equilateral consists of the control points from which the selected point is computed.

贝塞尔曲线下的动画效果相关推荐

  1. 贝塞尔曲线之购物车动画效果

    Question 贝塞尔曲线是什么? 贝塞尔曲线可以做什么? 怎么做? What is it ? 贝塞尔曲线在百度定义是贝塞尔曲线(Bézier curve),又称 贝兹 曲线或贝济埃曲线,是应用于二 ...

  2. 贝塞尔曲线与CSS3动画、SVG和canvas的应用

    简介 贝塞尔曲线是可以做出很多复杂的效果来的,比如弹跳球的复杂动画效果,首先加速下降,停止,然后弹起时逐渐减速的效果. 使用贝塞尔曲线常用的两个网址如下: 缓动函数:http://www.xuanfe ...

  3. Android利用贝塞尔曲线实现翻书效果（适配AndroidX）

    实现背景 不知道你有没有遇到同样的问题,要实现翻书效果,如果你是使用github上的demo或者好多博客上写的方式,你会发现,当api从28开始,会抛出Invalid Region.Op.REPLAC ...

  4. 纯CSS实现导航栏下拉动画效果

    实现思路 导航栏的下拉效果通过在ul的li里再嵌套一个ul,再通过animation属性改变第二导航栏ul的高度来实现导航栏下拉动画效果.老铁没毛病. 实现效果: HTML代码 <div cla ...

  5. CSS3技巧30：简单而实用的CSS导航下划线动画效果

    2021 结束了 迎来了 2022 回望这一年,收获了不少,也失去了很多. -------------------------------------------------------------- ...

  6. 手机端 自定义简单的下拉动画效果选择框 解决过渡失效

    手机端 自定义简单的下拉动画效果选择框 解决过渡失效 <template> // 弹出框触发 并显示选择结果<view class="header_top_sel" ...

  7. php超链接鼠标滑动加下划线,打造与众不同的鼠标滑过超链接下划线动画效果

    众所周知,超链接元素在默认情况下鼠标滑过时会出现一条下划线.默认的超链接下划线动画十分的生硬,我们可以通过一些简单的处理,来制作出带平滑过渡效果的超链接下划线动画效果. 先来体验一下这个超链接动画的效 ...

  8. css3贝塞尔曲线_CSS3动画–使用贝塞尔曲线创建具有弹跳效果的扇出

    您知道吗,可以使用transform CSS属性(例如缩放,倾斜和旋转)将动画转换添加到HTML元素中, ? 可以使用transition属性和@keyframes动画对它们进行动画@keyframe ...

  9. 贝塞尔曲线与CSS3动画、SVG和canvas的基情

    一.甚忙,短言之 最近谷歌那谁谁因为自己的相好被老大抢了,就去小米了!狗血的三角关系要比烂掉的TVB神剧好看多了. 但这只是小菜,贝塞尔曲线才是很角色,因为有外国血统,因此,和CSS3动画.SVG以及 ...

最新文章

  1. 支付宝何以支撑双十一4200万次/秒的数据库请求峰值？
  2. C语言程序设计第十章字符串,C语言程序设计（字符串）
  3. php禁止组合热键,cad组合快捷键命令有哪些
  4. 计算机病毒的八个特征,计算机病毒的五个特征- 1：.单项选择题(8)
  5. 记录 之 tf.data进行数据集处理常用的几个函数介绍
  6. @responseBody注解的使用
  7. 工作资讯004---多范式编程语言
  8. Python 变量赋值
  9. ArcGIS Maritime Server 开发教程（七）Maritime Server 正确的开发模式
  10. thymeleaf js 动态拼接html_Thymeleaf从入门到吃灰
  11. [云原生专题-3]：云平台 - 云计算平台快速入门
  12. u盘装华为服务器系统教程,华为服务器u盘重装系统
  13. 服务器遇到DDOS攻击怎么办？
  14. html的size属性,HTML size属性用法及代码示例
  15. c语言中如何识别空格键,在C++中如何判断“空格”键输入？
  16. vmware虚拟机删除光驱启动报错解决办法
  17. Servlet获取Excel中数据的两种方式
  18. Excel VBA：数据管理与维护
  19. 《流畅的python》这本确实老辣
  20. 矩阵取数游戏（动态规划）

热门文章

  1. [Linux]time+dd测试硬盘/手机/SD卡读写速度
  2. 三大通信协议（3）SPI——寄存器配置
  3. 强大的javascript
  4. 解决IE应用程序错误问题
  5. 关注朱令－－十年前铊中毒的女孩（本文转自http://www8.tianya.cn）
  6. tp6实现腾讯云存储与分片
  7. 计算机没有安装显卡驱动能显示桌面吗,电脑桌面右键没有显卡设置怎么添加
  8. 地下城与勇士服务器都在维护怎么办,DNF：停机维护却被洗号，刷了2个月的100ss全没了，都没异常提示...
  9. 关于IDEA2020.1插件市场加载不出来无法安装插件的解决办法
  10. 语音测试的软件是什么,直播软件语音前处理介绍