Gradient Boosting, Decision Trees and XGBoost with CUDA ——GPU加速5-6倍
xgboost的可以参考:https://xgboost.readthedocs.io/en/latest/gpu/index.html
整体看加速5-6倍的样子。
Gradient Boosting, Decision Trees and XGBoost with CUDA
 Gradient boosting is a powerful machine learning algorithm used to achieve state-of-the-art accuracy on a variety of tasks such as regression, classification and ranking. It has achieved notice in machine learning competitions in recent years by “winning practically every competition in the structured data category”. If you don’t use deep neural networks for your problem, there is a good chance you use gradient boosting.
Gradient boosting is a powerful machine learning algorithm used to achieve state-of-the-art accuracy on a variety of tasks such as regression, classification and ranking. It has achieved notice in machine learning competitions in recent years by “winning practically every competition in the structured data category”. If you don’t use deep neural networks for your problem, there is a good chance you use gradient boosting.
In this post I look at the popular gradient boosting algorithm XGBoost and show how to apply CUDA and parallel algorithms to greatly decrease training times in decision tree algorithms. I originally described this approach in my MSc thesis and it has since evolved to become a core part of the open source XGBoost library as well as a part of the H2O GPU Edition by H2O.ai.
H2O GPU Edition is a collection of GPU-accelerated machine learning algorithms including gradient boosting, generalized linear modeling and unsupervised methods like clustering and dimensionality reduction. H2O.ai is also a founding member of the GPU Open Analytics Initiative, which aims to create common data frameworks that enable developers and statistical researchers to accelerate data science on GPUs.
Gradient Boosting
The term “gradient boosting” comes from the idea of “boosting” or improving a single weak model by combining it with a number of other weak models in order to generate a collectively strong model. Gradient boosting is an extension of boosting where the process of additively generating weak models is formalised as a gradient descent algorithm over an objective function.
Gradient boosting is a supervised learning algorithm. This means that it takes a set of labelled training instances as input and builds a model that aims to correctly predict the label of each training example based on other non-label information that we know about the example (known as features of the instance). The purpose of this is to build an accurate model that can automatically label future data with unknown labels.
| Instance | Age | Has job | Owns house | Income ($1000) |
|---|---|---|---|---|
| 0 | 12 | N | N | 0 |
| 1 | 32 | Y | Y | 90 |
| 2 | 25 | Y | Y | 50 |
| 3 | 48 | N | N | 25 |
| 4 | 67 | N | Y | 35 |
| 5 | 18 | Y | N | 10 |
Table 1 shows a toy dataset with four columns: ”age”, “has job”, “owns house” and “income”. In this example I will use income as the label (sometimes known as the target variable for prediction) and use the other features to try to predict income.
To do this, first I need to come up with a model, for which I will use a simple decision tree. Many different types of models can be used for gradient boosting, but in practice decision trees are almost always used. I’ll skip over exactly how the tree is constructed. For now it is enough to know that it can be constructed in order to greedily minimise some loss function (for example squared error).
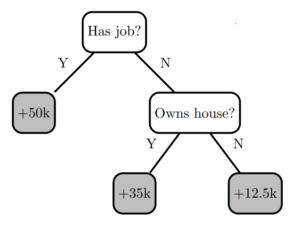 Figure 1. Decision tree 0.
Figure 1. Decision tree 0.
Figure 1 shows a simple decision tree model (I’ll call it “Decision Tree 0”) with two decision nodes and three leaves. A single training instance is inserted at the root node of the tree, following decision rules until a prediction is obtained at a leaf node.
This first decision tree works well for some instances but not so well for other instances. Subtracting the predicted label () from the true label (
) shows whether the prediction is an underestimate or an overestimate. This is called the residual and is denoted as
:
.
Table 2 shows the residuals for the dataset after passing its training instances through tree 0.
| Instance | Age | Has job | Owns house | Income ($1000) | Tree 0 Residuals |
|---|---|---|---|---|---|
| 0 | 12 | N | N | 0 | -12.5 |
| 1 | 32 | Y | Y | 90 | 40 |
| 2 | 25 | Y | Y | 50 | 0 |
| 3 | 48 | N | N | 25 | 12.5 |
| 4 | 67 | N | Y | 35 | 0 |
| 5 | 18 | Y | N | 10 | -40 |
 Figure 2. Decision tree 1.
Figure 2. Decision tree 1.
To improve the model, I can build another decision tree, but this time try to predict the residuals instead of the original labels. This can be thought of as building another model to correct for the error in the current model.
I add the new tree to the model, make new predictions and then calculate residuals again. In order to make predictions with multiple trees I simply pass the given instance through every tree and sum up the predictions from each tree.
| Instance | Age | Has job | Owns house | Income ($1000) | Tree 0 Residuals | Tree 1 Residuals |
|---|---|---|---|---|---|---|
| 0 | 12 | N | N | 0 | -12.5 | 5 |
| 1 | 32 | Y | Y | 90 | 40 | 22.5 |
| 2 | 25 | Y | Y | 50 | 0 | 17.5 |
| 3 | 48 | N | N | 25 | 12.5 | -5 |
| 4 | 67 | N | Y | 35 | 0 | -17.5 |
| 5 | 18 | Y | N | 10 | -40 | -22.5 |
Let’s take a look at the sum of squared errors for the extended model. SSE can be calculated as:
.
For the baseline model I just predict 0 for all instances.
| Model | SSE |
|---|---|
| No model (predict 0) | 6275 |
| Tree 0 | 1756 |
| Tree 0 + Tree 1 | 837 |
You can see that the error decreases as new models are added. To explain why fitting new models to the residuals of the current model increases the performance of the complete model, take the gradient of the SSE loss function for a single training instance:
.
So the residual is the negative gradient of the loss function for this training instance. Hence, by building models that adjust labels in the direction of these residuals, this is actually a gradient descent algorithm on the squared error loss function for the given training instances.
This minimises the loss function for the training instances until it eventually reaches a local minimum for the training data.
The XGBoost Algorithm
The above algorithm describes a basic gradient boosting solution, but a few modifications make it more flexible and robust for a variety of real world problems.
In particular, XGBoost uses second-order gradients of the loss function in addition to the first-order gradients, based on Taylor expansion of the loss function. You can take the Taylor expansion of a variety of different loss functions (such as logistic loss for binary classification) and plug them into the same algorithm for greater generalisation.
In addition to this, XGBoost transforms the loss function into a more sophisticated objective function containing regularisation terms. This extension of the loss function adds penalty terms for adding new decision tree leaves to the model with penalty proportional to the size of the leaf weights. This inhibits the growth of the model in order to prevent overfitting. Without these regularisation terms, gradient boosted models can quickly become large and overfit to noise present in the training data. Overfitting means that the model may look very good on the training set but generalises poorly to new data that it has not seen before.
You can find a more detailed mathematical explanation of the XGBoost algorithm in the documentation.
Quantiles
In order to explain how to formulate a GPU algorithm for gradient boosting, I will first compute quantiles for the input features (‘age’, ‘has job’, ‘owns house’). This process involves finding cut points that divide a feature into equal-sized groups. The boolean features ‘has job’ and ‘owns house’ are easily transformed by using 0 to represent false and 1 to represent true. The numerical feature ‘age’ transforms into four different groups.
| Age | Quantile | Count |
|---|---|---|
| <18 | 0 | 1 |
| <32 | 1 | 2 |
| <67 | 2 | 2 |
| 67+ | 3 | 1 |
The following table shows the training data with quantised features.
| Instance | Age | Has job | Owns house |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 2 | 1 | 1 |
| 2 | 1 | 1 | 1 |
| 3 | 2 | 0 | 0 |
| 4 | 3 | 0 | 1 |
| 5 | 1 | 1 | 0 |
It turns out that dealing with features as quantiles in a gradient boosting algorithm results in accuracy comparable to directly using the floating point values, while significantly simplifying the tree construction algorithm and allowing a more efficient implementation.
Finding Splits in Decision Trees
Here’s a brief explanation of how to find appropriate splits for a decision tree, assuming SSE is the loss function. As an example, I’ll try to find a decision split for the “age” feature at the start of the boosting process. After quantisation there are three different possible splits I could create for this feature: (age < 18), (age < 32) or (age < 67). I need a way to evaluate the quality of each of these splits with respect to the loss function in order to pick the best.
Given a node in a tree that currently contains a set of training instances and makes a prediction
(this prediction value is also called the leaf weight), I can re-express the loss function at boosting iteration
as follows with
as the prediction so far for instance
and
as the weight predicted for that instance in the current tree:
.
Rewritten in terms of the residuals and expanded this yields
.
I can simplify here by denoting the sum of residuals in the leaf as
.
.
The above equation gives the training loss of a set of instances in a leaf. The next question is, what value should I predict in this leaf to minimise the loss function? The optimal leaf weight is given by setting
.
This gives
.
I can plug this back into the loss function for the current boosting iteration to see the effect of predicting in this leaf:
.
Simplifying, I get
.
This equation tells what the training loss will be for a given leaf , but how does it tell me if one split is better than another? When I create a split in the training instances
, I denote the set of instances going down the left branch as
and those going down the right branch
. I predict
in the left leaf and
in the right leaf.
.
The above equation gives the training loss for a given split in the tree, so I can simply apply this function to a number of possible splits under consideration and choose the one with the lowest training loss. I can recursively create new splits down the tree until I reach a specified depth or other stopping condition.
Note that the sum term never actually changes at boosting iteration
and can be ignored for the purpose of determining if one split is better than another in the current tree. This means that, despite all of the equations, I only need the sum of the residuals in the left-hand branch (
), the sum of the residuals in the right-hand branch (
) and the number of examples in each (
,
) to evaluate the relative quality of a split. I call this reduced function the “split loss”:
.
Implementation: Histograms and Prefix Sums
Bringing this back to my example of finding a split for the feature “age”, I’ll start by summing the residuals for each possible quantile value of age. Assume I’m at the start of the boosting process and therefore the residuals are equivalent to the original labels
.
The sums for each quantile can be calculated easily in CUDA using simple global memory atomic add operations or using the more sophisticated shared memory histogram algorithm discussed in this post.
In order to apply the function, I need to know the sum of all values to the left and all values to the right of possible split points. To do this I can use the ever useful parallel prefix sum (or scan) operation. In this case I use the “inclusive” variant of scan for which efficient implementations are available in the thrust and cub libraries. I also make the reasonable assumption that I know the sum of all residuals in the current set of instances (210 here). This allows me to calculate the sum of elements to the right by subtracting the elements to the left (the inclusive scan) from the total.
| Quantile | <18 | <32 | <67 | 67+ |
|---|---|---|---|---|
|
|
1 | 2 | 2 | 1 |
|
Quantile sum |
0 | 60 | 115 | 35 |
|
Inclusive scan |
1 | 3 | 5 | 6 |
|
Inclusive scan |
0 | 60 | 175 | 210 |
| Split loss | -4410 | -4350 | -3675 | – |
After applying the split loss function to the dataset, the split (<18) has the greatest reduction in the SSE loss function.
I would also perform this test over all other features and then choose the best out of all features to create a decision node in the tree. A GPU can do this in parallel for all nodes and all features at a given level of the tree, providing powerful scalability compared to CPU-based implementations.
Memory Efficiency: Bit Compression and Sparsity
Gradient boosting in XGBoost contains some unique features specific to its CUDA implementation. Memory efficiency is an important consideration in data science. Datasets may contain hundreds of millions of rows, thousands of features and a high level of sparsity. Given that device (GPU) memory capacity is typically smaller than host (CPU) memory, memory efficiency is important.
I have implemented parallel primitives for processing sparse CSR (Compressed Sparse Row) format input matrices following work in the modern GPU library and CUDA implementation of sparse matrix vector multiplication algorithms. These primitives allow me to process a sparse matrix in CSR format with one work unit (thread) per non-zero matrix element and efficiently look up the associated row index of the non-zero element using a form of vectorised binary search. This significantly reduces storage requirements, provides stable performance and still allows very clean and readable code.
Another innovation is the use of symbol compression to store the quantised input matrix on the device. The maximum integer value contained in a quantised nonzero matrix element is proportional to the number of quantiles, commonly 256, and to the number of features which are specified at runtime by the user. It seems wasteful to use a four-byte integer to store a value that very commonly has a maximum value less than 216. To solve this, the input matrix is bit compressed down to bits per element on the host before copying it to the device. Note that this data is not modified once on the device and is read many times.
I can then define an iterator that accesses these compressed elements in a seamless way, resulting in minimal changes to existing CUDA kernels and function calls:
CompressedIterator<int> itr(compressed_buffer, max_value); template <typename iter_t> __global__ void some_kernel(iter_t x) { int tid = threadIdx.x + blockIdx.x * blockDim.x; int decompressed_value = x[tid]; }
It’s easy to implement this compressed iterator to be compatible with the Thrust library, allowing the use of parallel primitives such as scan:
thrust::device_vector<int> output(n); thrust::exclusive_scan(itr, itr + n, output.begin());
Using this bit compression method in XGBoost reduces the memory cost of each matrix element to less than 16 bits in typical use cases. This is half the cost of the equivalent CPU implementation. Note that while it would be possible to use this iterator just as easily on the CPU, the instructions required to extract a symbol from the compressed stream can result in a noticeable performance penalty. The GPU kernels are typically memory bound (as opposed to compute bound) and therefore do not incur the same performance penalty from extracting symbols.
Performance on GPUs
I evaluate performance of the entire boosting algorithm using the commonly benchmarked UCI Higgs dataset. This is a binary classification problem with 11M rows * 29 features and is a relatively time consuming problem in the single machine setting.
The following Python script runs the XGBoost algorithm. It outputs the decreasing test error during boosting and measures the time taken by GPU and CPU algorithms.
import csv
import numpy as np import os.path import pandas import time import xgboost as xgb import sys if sys.version_info[0] >= 3: from urllib.request import urlretrieve else: from urllib import urlretrieve data_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/00280/HIGGS.csv.gz" dmatrix_train_filename = "higgs_train.dmatrix" dmatrix_test_filename = "higgs_test.dmatrix" csv_filename = "HIGGS.csv.gz" train_rows = 10500000 test_rows = 500000 num_round = 1000 plot = True # return xgboost dmatrix def load_higgs(): if os.path.isfile(dmatrix_train_filename) and os.path.isfile(dmatrix_test_filename): dtrain = xgb.DMatrix(dmatrix_train_filename) dtest = xgb.DMatrix(dmatrix_test_filename) if dtrain.num_row() == train_rows and dtest.num_row() == test_rows: print("Loading cached dmatrix...") return dtrain, dtest if not os.path.isfile(csv_filename): print("Downloading higgs file...") urlretrieve(data_url, csv_filename) df_higgs_train = pandas.read_csv(csv_filename, dtype=np.float32, nrows=train_rows, header=None) dtrain = xgb.DMatrix(df_higgs_train.ix[:, 1:29], df_higgs_train[0]) dtrain.save_binary(dmatrix_train_filename) df_higgs_test = pandas.read_csv(csv_filename, dtype=np.float32, skiprows=train_rows, nrows=test_rows, header=None) dtest = xgb.DMatrix转载于:https://www.cnblogs.com/bonelee/p/10734009.html
Gradient Boosting, Decision Trees and XGBoost with CUDA ——GPU加速5-6倍相关推荐
- 机器学习论文:《LightGBM: A Highly Efficient Gradient Boosting Decision Tree》
翻译自<LightGBM: A Highly Efficient Gradient Boosting Decision Tree> 摘要 Gradient Boosting Decisio ...
- Lightgbm源论文解析:LightGBM: A Highly Efficient Gradient Boosting Decision Tree
写这篇博客的原因是,网上很多关于Lightgbm的讲解都是从Lightgbm的官方文档来的,官方文档只会告诉你怎么用,很多细节都没讲.所以自己翻过来Lightgbm的源论文:LightGBM: A H ...
- 《LightGBM: A Highly Efficient Gradient Boosting Decision Tree》论文笔记
1 简介 本文根据2017年microsoft研究所等人写的论文<LightGBM: A Highly Efficient Gradient Boosting Decision Tree> ...
- 『 论文阅读』LightGBM原理-LightGBM: A Highly Efficient Gradient Boosting Decision Tree
17年8月LightGBM就开源了,那时候就开始尝试上手,不过更多还是在调参层面,在作者12月论文发表之后看了却一直没有总结,这几天想着一定要翻译下,自己也梳理下GBDT相关的算法. Abstract ...
- 机器学习算法系列(二十)-梯度提升决策树算法(Gradient Boosted Decision Trees / GBDT)
阅读本文需要的背景知识点:自适应增强算法.泰勒公式.One-Hot编码.一丢丢编程知识 一.引言 前面一节我们学习了自适应增强算法(Adaptive Boosting / AdaBoost Alg ...
- GBDT(Gradient Boosting Decision Tree
GBDT(Gradient Boosting Decision Tree) 又叫 MART(Multiple Additive Regression Tree),是一种迭代的决策树算法,该算法由 ...
- Gradient Boosted Decision Trees详解
感受 GBDT集成方法的一种,就是根据每次剩余的残差,即损失函数的值.在残差减少的方向上建立一个新的模型的方法,直到达到一定拟合精度后停止.我找了一个相关的例子来帮助理解.本文结合了多篇博客和书,试图 ...
- Gradient Boosting Decision Tree学习
Gradient Boosting Decision Tree,即梯度提升树,简称GBDT,也叫GBRT(Gradient Boosting Regression Tree),也称为Multiple ...
- LightGBM: A Highly Efficient Gradient Boosting Decision Tree
论文杂记 图像检索--联合加权聚合深度卷积特征的图像检索方法 主目录 下一篇 文章结构 lightgbm原理 [前言] LightGBM: A Highly Efficient Gradient Bo ...
最新文章
- rust如何进枪战服_天龙八部怀旧服九大门派详细打造攻略——少林篇
- [Usaco2007 Dec]宝石手镯[01背包][水]
- 关于Oracle的提示详解(1)
- JAVA中堆和栈的区别
- Windows环境下 node 取消 npm install 采用软连接引用node_modules
- llnmp 环境一键部署 2种安装方法
- Filter过滤器概念及生命周期
- mysql中文版下载5.6_mysql5.6官方版下载
- vc与三菱PLC编程口通信C语言源代码,三菱PLC通讯与编程实例!
- 判断图同构大杀器---nauty算法
- BZOJ2434: [Noi2011]阿狸的打字机
- 世界上最著名的24句哲理
- 获取JOP卡的版本与功能信息
- java.lang.IllegalArgumentException 异常报错完美解决
- unity3D学习之音频数据的采集要点-audio菜鸟笔记6
- CV中一些常见的特征点
- 可可西里-昨夜,真实让我感动!
- 「镁客早报」华为余承东欢迎苹果使用5G芯片;三星首款折叠手机本月开卖
- 绘制思维导图用什么软件?告诉你三个实用的软件
- RTOS 系统篇-统计任务的 CPU 使用率
热门文章
- nginx获取函数执行调用关系
- 上海大学c语言基础题目,求c语言大神学长学姐解答题目
- python中的浮点数用法_如何利用Python在运算后得到浮点数值的方法详解
- arttemplate 不转义html,使用artTemplate模板引擎渲染错误
- mysql报错:Column 'id' in field list is ambiguous,以及tp的三表联合查询语句,打印sql等
- mysql中的where,group by,having:
- 【机器学习入门到精通系列】SVM与核函数(附程序模拟!)
- 【Java Web开发指南】redis笔记
- python【力扣LeetCode算法题库】289- 生命游戏
- java多图片上传json_[Java教程]SpringMVC框架五:图片上传与JSON交互
