Gram-Schmidt正交化

在前面的几个最小二乘的文章中，实际上已经看到Gram-Schmidt正交化的影子。在我个人看来，Gram-Schmidt正交化更像是一种最小二乘的简化算法。下面，我会接着上一篇文章中的最后一个例子讲，慢慢引出Gram-Schmidt的想法 ——> 那就是如何“改写”矩阵A中的列向量? 最大程度简化最小二乘的求解过程。

在上一篇文章的最后一个例子中，给出了和不为0的三个时间点t=(1,3,5)的直线拟合问题b=C+Dt(先不考虑三个时间点所对应的值b)。当时，为了让正规方程更好解，通过把t减去他的均值3，得到T=t-3=(-2,0,2)，实现了最小二乘解的快速求解。也就是不再需要机械的通过套用公式来计算，而是直接求解简化后的正规方程，就能得到答案，同时也避免了求的逆，这种精度误差较大的运算。下面，我们详细的介绍一下上述过程。

首先，对于三个数据点(t1=1,b1=1),(t2=3,b2=2),(t3=5,b3=4)而言，对应的矩阵A为：

矩阵A的两个列向量的内积不为0，不正交

如下图所示：

Matlab code:

close all
clear all%时间t=[1 3 5]不在0的两侧，A中的两个列向量不正交，生成的A'A不是主对角线左右两边都是0的对角阵
A=[1 1 1;1 3 5]'
b=[1 2 4]'col1=A(:,1)
col2=A(:,2)col1'*col2A'*A%plot
X=[0,0];
Y=[0,0];
Z=[0,0];
U=[1,1];
V=[1,3];
W=[1,5];quiver3(X,Y,Z,U,V,W,0,'LineWidth',1)
axis equal
legend('Col1,Col2','Location','northwest')

且b不在A的列空间内，原方程组无解，需要通过最小二乘法来求近似解。套用公式得到，其中与的逆分别为：

方程的近似解为：

套用公式，投影p为：

接下来，我们令t=(1,3,5)减去均值，变成了T=(-2,0,2)，矩阵A也变成了：

两个列向量的内积为0，矩阵A的两个列向量也从非正交变成了正交

如下图所示：

Matlab code:

%时间t=[-2 0 2]位于0的两侧对称，A中的两个列向量彼此正交，A'A可以生成主对角线左右两边都是0的对角阵
A=[1 1 1;-2 0 2]'col1=A(:,1)
col2=A(:,2)col1'*col2A'*A%plot
Q1=[1,-2];
Q2=[1,0];
Q3=[1,2];
hold on
quiver3(X,Y,Z,Q1,Q2,Q3,0,'LineWidth',2)legend('Col1,Col2','New Col1,New Col2','Location','northwest')

同时，我们还发现，如果矩阵A中的列向量彼此正交，那么就变成了对角阵：

补充：

且对角阵有如下性质：

这就是说，通过这一步对矩阵A的改变，达到了简化了计算近似解的目的，同时也简化了投影向量p的计算。因为为对角阵，所以我们可以直接写出的逆，即，直接取所有对角线元素的倒数：

方程的近似解，也变成了：

套用公式，投影p仍然是：

注意：矩阵A的改变虽然改变了，但投影p不变。（这说明，对于矩阵A的改变没有A的列空间，即从A=[1 1 1;；1 3 5]'到A=[1 1 1；-2 0 2]'，矩阵的A的列空间是一样的。因为，如果对他们进行高斯消元，得到的最简行阶梯矩阵是一样的=[1 0 0,0 1 0]'）

更进一步，如果我们把A中的两个彼此正交的列向量(orthogonal vectors)都变成单位正交向量(orthogonal unit vectors)，则会从对角阵变成单位矩阵I，的逆也变成了单位矩阵。

把矩阵A中已经彼此正交的向量，变成单位正交向量的方法是：把A中的每一个向量进行单位化（也叫归一化），即，该向量除以这个向量自身的长度。

根据向量长度的计算公式，列向量col1的长度为，col2的长度为，归一化后有：

内积为0，彼此正交：

如下图所示：

Matlab code:

%把矩阵A中的两个相互正交的列向量变成单位向量，这样一来，A也变成了标准正交矩阵
Length_Col1 = sqrt(sum(col1.^2));
Length_Col2 = sqrt(sum(col2.^2));
col1_unit=col1./Length_Col1
col2_unit=col2./Length_Col2A_unit=[col1_unit col2_unit]% check:对于标准正交矩阵而言，有A'A=I
A_unit'*A_unit%plot
Q1=[1/Length_Col1,-2/Length_Col2];
Q2=[1/Length_Col1,0/Length_Col2];
Q3=[1/Length_Col1,2/Length_Col2];
hold on
quiver3(X,Y,Z,Q1,Q2,Q3,0,'LineWidth',2)legend('Col1,Col2','NewCol1,NewCol2','Unit NewCol1,Unit NewCol2','Location','northwest')

单位化后，矩阵A又变成了矩阵：

以及，新的方程：(注意：为了维持原方程组Ax=b中的A变成后，方程左右两边保持不变，原方程中的x也要改，变成)

现在，基于这个新矩阵生成正规方程，右边的计算结果就是单位矩阵I：

正规方程左边：

也就是说，当矩阵A中的列向量变成单位正交向量后，极大的简化了近似解的计算。因为为单位矩阵，使得原来的正规方程变成了：

与此同时，近似解的计算公式也被极大地简化了：

最终得到的答案和之前一样：

在本例中，归一化后的两个相互正交的单位列向量和是一组标准正交基。

Matlab code:

%% 用简化后的公式计算正规方程的解
%x=Q'b
x=A_unit'*bx_new=[x(1)/Length_Col1; x(2)/Length_Col2]%P=QQ'
P=A_unit*A_unit'%projection p=QQ'b
p=P*b

标准正交基(Orthonormal Bases)

现在，我们给出关于标准正交基Orthonormal的正式定义：

如果一组列向量，他们满足彼此之间的内积为0(正交性)，且，他们的长度都为1(归一化)。则，我们把这样的一组列向量称为标准正交基Orthonomal。同时，我们也把由标准正交基组成的矩阵用大写的英文字母Q来表示。

对于标准正交基而言，一个最常见的例子就是x-y二维坐标系。x轴和y轴不仅相互垂直，坐标轴上的每一个刻度都是该轴所对应的单位向量的长度的倍数(如果用q1=(1,0)表示x轴的单位向量，用q2=(0,1)表示y轴的单位向量的话)。q1和q2共同组成了一个2x2矩阵Q，这是一个2x2的单位矩阵。

对于n维空间，同样有n个坐标轴e1,e2,....en，他们也是一组标准正交基，且他们所组成的矩阵Q也是一个单位阵。

标准正交矩阵(Orthogonal Matrices)

我们把用标准正交基q1,q2...qn所组成的矩阵称为标准正交矩阵Q，Q可以是方阵也可以不是方阵。且，。

如果标准正交矩阵Q是一个方阵的话，则有：

也就是说，如果方阵Q是一个标准正交矩阵，则方阵Q的转置就是Q的逆矩阵。

例：任何置换矩阵P(permutation)都是一个标准正交矩阵。

上图的两个置换矩阵，分别交换了(x,y,z)的位置和交换了(x,y)的位置。因为，这两个置换矩阵P的列向量都是单位向量，且彼此两两正交。所以也是标准正交矩阵。

最后，在这里补充一条标准正交矩阵Q的又一条重要性质，即，用一个标准正交矩阵Q去乘一个任意向量都不会改变这个向量的长度。（书上上，这一性质还挺重要的，只是我暂时没发现）

标准正交矩阵的投影与最小二乘

对于一个mxn的矩阵A，如果矩阵A中的列向量都彼此正交，且向量长度都是1。则A是一个标准正交矩阵。若方程组Ax=b无解，则需要根据最小二乘的计算公式分别计算和。但如果A是标准正交矩阵Q的话，或者说，如果我们预先把原本不是标准正交矩阵的矩阵A变成标准正交矩阵Q的话，就能极大的简化最小二乘的计算。如下图所示，下图中横线处都是原来需要计算的部分，因为标准正交矩阵的性质，都变成了单位矩阵I，等同于不再需要计算了。

也就是说，如果我们能够在计算任意矩阵A的最小二乘解之前，预先把A改造成标准正交矩阵Q，则能够带来以下的一些计算上的简化与便利。：

第一：他极大地简化了正规方程的表达式，同时，直接给出了最小二乘解。

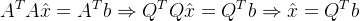（正规方程）

第二：他简化了所有包含的计算，同时，更重要的是他也避免了求的逆。

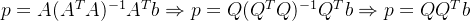（投影）

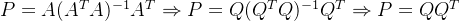（投影矩阵）

标准正交矩阵Q所带来的影响，并不仅仅体现在简化计算公式上，在投影的几何表示上也有相应的体现。当A为正交矩阵Q时，向量的投影()可写成在每一个列向量上的投影的和的形式：

其中：

依此类推。。。

令b=(b1,b2,...,bn),则有：

依此类推。。。

用几何图像来表示就是：

也就是说，向量b在A所张成的列空间上的投影p等于，b在每个坐标轴上的投影的和。

此外，当A为标准正交矩阵时(当A为方阵时,m=n)，A中的列向量可以张满整个。A中的每个列向量，实际上就是n维正交坐标系中的每个轴所对应的单位向量。对于中的任意一个向量b，b在A的列空间内，所以可以写成Ax=b的形式，x中的每个元素都是A中各列所对应的权重。当A为Q时，我们把Qx=b写成如下形式：

q1,q2,...,qn分别表示n维坐标系中的每个坐标轴上的单位向量，这样一来，上式所表示的就是，在n维直角坐标系中，任意一个向量b等于，他在q1轴，q2轴，。。。qn轴上分量的和。

例如：

当x=1.5,y=1,z=2时有。

小结：

1, 给定的mxn方程组 Ax=b 无解

2, 左右两边同时乘以，得到正规方程

3, 求解正规方程，得到

4, 若A是一个标准正交矩阵Q，则改Ax=b为Qx=b

5, 左右两边同时乘以,得到新的正规方程

6, 极大的简化了原来计算，得到

7, 与此同时，也简化了投影p的计算，得到

（全文完）

作者 --- 松下J27

参考文献(鸣谢)：

1，Introduction to Linear Algebra，Fifth Edition - Gilbert Strang

2，线性代数及其应用，候自新，南开大学出版社 1990

3，Linear Algebra and Its Applications, Second Edition, Gilbert Strang, 1980

4，Linear Algebra and Its Applications, Fourth Edition, Gilbert Strang, 2005

增加了插图和对应的matlab代码，2023/05/24

对全文进行了大量的修改。2023/06/25

（配图与本文无关）

线性代数 --- Gram-Schmidt, 格拉姆-施密特正交化（上）相关推荐

漫步线性代数十七——正交基和格拉姆-施密特正交化(上)
对于一个正交基,每个向量和其他所有向量垂直,坐标轴就是互相正交的.我们还可以进一步改善:每个向量除以它的长度得到单位向量,这样的话正交基变成了标准正交基: 16.如果 qTiqj={01i≠j,给出正 ...
漫步线性代数十八——正交基和格拉姆-施密特正交化(下)
格拉姆-施密特声明:以后博主会把文章的pdf版本陆续发布到的网上,免费供大家下载正交基和格拉姆-施密特正交化假设我们有是是三个无关向量a,b,ca,b,c,如果他们是正交的,那么会多问题都变得容 ...
matlab格拉姆施密特,改进的格拉姆-施密特正交化（modified Gram-Schmidt Process）
最近在重新学习线性代数,学习的教材是MIT Gilbert Strang 教授的<INTRODUCTION TO LINEAR ALGEBRA>,在第4.4章节格拉姆-施密特正交化时,书中 ...
施密特正交化_格拉姆-施密特正交化--QR分解法的来源
人类的数学发展到了今天,已经如浩瀚的宇宙般深不见底,不管时代怎么变迁,数学总是以超前于人类的科技水平而存在,如果说宇宙有尽头的话,那么宇宙的尽头也是数学的尽头,数学的停止就是世界的末日.所以我后悔当初 ...
线性代数 --- Gram-Schmidt, 格拉姆-施密特正交化（下）
Gram-Schmidt正交化过程到目前为止,我们都是在反复强调"对于无解的方程组Ax=b而言,如果矩阵A是标准正交矩阵的话,就怎么怎么好了....".因为,不论是求投影还是计算 ...
线性代数(三十九) ：格拉姆-施密特正交化与标准正交基
本节介绍正交的概念,以及将基变为正交基的格拉姆-施密特(Gram-Schmidt)方法 1 正交如果向量x,y满足: 则称x与y正交(orthogonal)或者垂直(perpendicular),记 ...
施密特正交化_机器学习线性代数基础 | 3.3施密特正交化：寻找最佳投影基
▼ 更多精彩推荐,请关注我们 ▼3.3 施密特正交化:寻找最佳投影基在本章的前面两个小节里,我们通过向指定子空间进行投影,探索到了如何寻找"最近距离"的有效途径,通过理论分析和 ...
通俗理解“Schmidt正交化”和“正交矩阵” 此博文包含图片 (2015-05-19 09:50:47) 施密特正交化在空间上是不断建立垂直于原次维空间的新向量的过程。如图β2垂直于β1（1维）
通俗理解"Schmidt正交化"和"正交矩阵" 施密特正交化在空间上是不断建立垂直于原次维空间的新向量的过程. 如图β2垂直于β1(1维)构建新2维,β3垂直于 ...
线性代数学习笔记——第七十讲——格拉姆—施密特（Gram-Schmidt）正交化方法
1. 格拉姆-施密特(Gram-Schmidt)正交化方法详解 2. 格拉姆-施密特(Gram-Schmidt)正交化示例

线性代数 --- Gram-Schmidt, 格拉姆-施密特正交化（上）

Gram-Schmidt正交化

标准正交基(Orthonormal Bases)

标准正交矩阵(Orthogonal Matrices)

标准正交矩阵的投影与最小二乘

（正规方程）

（投影）

（投影矩阵）

小结：

线性代数 --- Gram-Schmidt, 格拉姆-施密特正交化（上）相关推荐

最新文章

热门文章